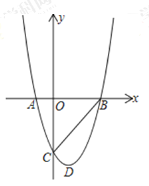
题目内容
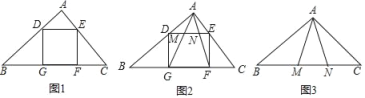
【题目】(1)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,若AB=AC=2,求DE的长;
(2)如图,在(1)的条件下,连结AG、AF分别交DE于M、N两点,求MN的长;
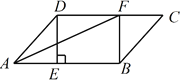
(3)如图,在△ABC中,AB=AC=BN=2,∠BAC=108°,若AM=AN,请直接写出MN的长.
【答案】(1)DE=![]() ;(2)MN=
;(2)MN=![]() ;(3)MN=3﹣
;(3)MN=3﹣![]() .
.
【解析】
(1)先利用勾股定理求出BC的长,然后证明△BGD和△EFC是等腰直角三角形,根据正方形的性质可得BG=FG=FC即可解决问题.
(2)利用平行线分线段成比例定理,构建方程即可解决问题.
(3)证明BM=AM=AN,设MN=x,则AN=AM=BM=2-x.由△NAM∽△NBA,可得AN2=NMNB,构建方程即可解决问题.
(1)解:∵AB=AC=2,∠A=90°,
∴∠B=∠C=45°,BC=![]() ,
,
∵四边形DEFG是正方形,
∴DE=DG=GF=EF,∠DGF=∠EFG=90°,
∴∠BGD=∠CFE=90°,
∴∠B=∠BDG=45°,∠C=∠CEF=45°,
∴BG=DG, CF=EF,
∴BG=FG=FC=DE,
∴DE=![]() BC=
BC=![]() .
.
(2)∵DE∥BC,
∴![]() ,
,
∴![]() ,
,
∴MN=![]() .
.
(3)∵AB=AC,∠BAC=108°,
∴∠B=∠C=36°,
∵BA=NB,
∴∠ANB=∠BAN=72°,
∵AM=AN,
∴∠AMN=∠ANM=72°,
∴∠B=∠BAM=∠MAN=36°,
∴BM=AM=AN,设MN=x,则AN=AM=BM=2﹣x.
∵△NAM∽△NBA,
∴AN2=NMNB,
∴(2﹣x)2=2x,
∴x=3﹣![]() 或3+
或3+![]() (舍弃)
(舍弃)
∴MN=3﹣![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目