题目内容
13.有五张分别标有数字-3,-1,0,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记该张卡片上的数字为k,则使分式方程$\frac{x}{x-1}-2=\frac{k}{1-x}$有正数解,且以x为自变量的二次函数y=x2-(k2+1)x-k+2的图象不经过点(1,0)的概率是$\frac{3}{5}$.分析 先求出分式方程的解,再找出使分式方程有正整数解的数,然后得到使二次函数y=x2-(k2+1)x-k+2的图象不经过点(1,0)的k的值,最后根据概率公式进行计算即可.
解答 解:∵方程$\frac{x}{x-1}-2=\frac{k}{1-x}$的解是x=k+2,
∴-1,0,1,2能使方程有正整数解,
∵以x为自变量的二次函数y=x2-(k2+1)x-k+2的图象不经过点(1,0),
∴12-(k2+1)-k+2≠0,
∴k≠1且k≠-2,
∴满足条件的k只有-1,0,和2,
∴使关于x的一元二次方程$\frac{x}{x-1}-2=\frac{k}{1-x}$有两个不相等的实数根,且以x为自变量的二次函数y=x2-(k2+1)x-k+2的图象不经过点(1,0)的概率是$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
4.下列运算错误的是( )
| A. | -(a-2b)=-a+2b | B. | a2•a3=a5 | C. | (a-2)2=a2+4 | D. | 3a-2a=a |
8.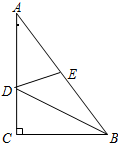 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )| A. | $\frac{\sqrt{10}}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{3}{2}$ |
5.为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
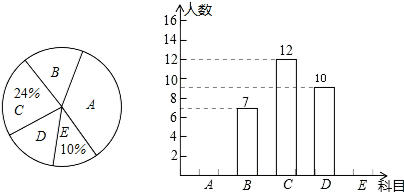

| A. | 选科目E的有5人 | |
| B. | 选科目D的扇形圆心角是72° | |
| C. | 选科目A的人数占体育社团人数的一半 | |
| D. | 选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6° |
3.在一个不透明的袋子中,装有红球、黄球、篮球、白球各1个,这些球除颜色外无其他差别,从袋中随机取出一个球,取出红球的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 1 |
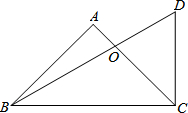 一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.
一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.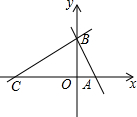 如图,平面直角坐标系中,直线y=-$\sqrt{3}x$+$\sqrt{3}$与坐标轴分别交于点A、B,且点C在x轴负半轴上,且AB:AC=1:2.
如图,平面直角坐标系中,直线y=-$\sqrt{3}x$+$\sqrt{3}$与坐标轴分别交于点A、B,且点C在x轴负半轴上,且AB:AC=1:2.