题目内容
 如图,点O为正方形ABCD的对角线交点,PE⊥BC,求证:△APD∽△OEC.
如图,点O为正方形ABCD的对角线交点,PE⊥BC,求证:△APD∽△OEC.考点:相似三角形的判定,正方形的性质
专题:证明题
分析:根据正方形的性质得出AD=DC,∠DOC=∠DCB=90°,∠ADP=∠CDP=∠OCE=45°,证△ADP≌△CDP,推出∠DAP=∠DCP,求出∠DAP=∠EOC,根据相似三角形的判定推出即可.
解答:证明:∵四边形ABCD是正方形,
∠ADP=∠CDP=∠OCE=45°,AD=DC,
在△ADP和△CDP中,
,
∴△ADP≌△CDP(SAS),
∴∠DAP=∠DCP,
∵四边形ABCD是正方形,PE⊥BC,
∴∠PEB=∠DCB=90°,
∴PE∥DC,
∴∠DCP=∠CPE=∠DAP,
∵四边形ABCD是正方形,PE⊥BC,
∴∠DOC=∠PEC=90°,
∴P、O、E、C四点共圆,
∴∠EOC=∠CPE,
∴∠EOC=∠DAP,
∵∠ADP=∠OCE=45°,
∴△APD∽△OEC.
∠ADP=∠CDP=∠OCE=45°,AD=DC,
在△ADP和△CDP中,
|
∴△ADP≌△CDP(SAS),
∴∠DAP=∠DCP,
∵四边形ABCD是正方形,PE⊥BC,
∴∠PEB=∠DCB=90°,
∴PE∥DC,
∴∠DCP=∠CPE=∠DAP,
∵四边形ABCD是正方形,PE⊥BC,
∴∠DOC=∠PEC=90°,
∴P、O、E、C四点共圆,
∴∠EOC=∠CPE,
∴∠EOC=∠DAP,
∵∠ADP=∠OCE=45°,
∴△APD∽△OEC.
点评:本题考查了相似三角形的判定定理,正方形的性质,圆内接四边形的性质,平行线的性质和判定的应用,解此题的关键是推出∠EOC=∠DAP,∠ADP=∠OCE=45°,注意:①有两个角对应相等的两三角形相似.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
下列四个数中最小的是( )
| A、0 | ||
| B、0.5 | ||
| C、-1 | ||
D、
|
多项式4x2+1加上一个数或单项式后,使它称为一个整式的完全平方,那么加上的数或单项式可从①-1②4x③-4x④-4x2中选取( )
| A、② | B、③ | C、②③ | D、①②③④ |
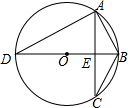 已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程ax2+bx-c=0是关于x的一元二次方程.
已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程ax2+bx-c=0是关于x的一元二次方程. 已知AB,AC为弦,OM⊥AB于M,ON⊥AC于N,求证:MN∥BC且MN=
已知AB,AC为弦,OM⊥AB于M,ON⊥AC于N,求证:MN∥BC且MN=