题目内容
19.若$\frac{b+c}{a}=\frac{c+a}{b}$=$\frac{a+b}{c}$=k,求k3的值.分析 ①根据等比性质,可得k的值,再根据乘方的意义,可得答案;②根据分式的性质,可得 k的值,再根据乘方的意义,可得答案.
解答 解:①a+b+c≠0时,k=$\frac{b+c+c+a+a+b}{a+b+c}$=2,
k3=23=8;
②a+b+c=0时,a+b=-c,
k=$\frac{a+b}{c}$=$\frac{-c}{c}$=-1,
k3=(-1)3=-1,
综上所述:k3的值是8或-1.
点评 本题考查了比例的性质,利用等比性质是解题关键,要分类讨论,以防遗漏.

练习册系列答案
相关题目
9.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,说明它是假命题的反例可以是( )
| A. | ∠1=50°,∠2=40° | B. | ∠1=50°,∠2=50° | C. | ∠1=40°,∠2=40° | D. | ∠1=∠2=45° |
10.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (b-a)2=b2-2ab+a2 | C. | (a+2b)(a-2b)=a2-2b2 | D. | (a-b)2=a2-2ab-b2 |
4.国庆期间,某公园门票规定如下表:
某校七年级(1)(2)两个班共104人去游园,如果以班为单位购票,共付1240元,其中(1)班人数大于40人小于50人,试问:
(1)这两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票最省钱?
| 购票人数 | 1-50张 | 51~100张 | 100张以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
(1)这两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票最省钱?
11.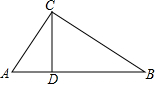 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )| A. | BD=a•sinα | B. | AD=$\frac{a•sinα}{tanα}$ | C. | AC=$\frac{a}{sinα}$ | D. | CD=a•cosα |
8.下列因式分解正确的是( )
| A. | a2b-2a3=a(ab-2a2) | B. | x2-x+$\frac{1}{4}$=${(x-\frac{1}{2})}^{2}$ | C. | x2+2x+1=x(x+2)+1 | D. | 4x2-y2=(4x+y)(4x-y) |