题目内容
要锻造一个直径为12cm,高为8cm的圆柱形毛坯,应截取多少直径为8cm的圆钢?(不计锻造时的损耗)
(1)本题建立方程的相等关系是______.
(2)设______,根据数量关系填表:
| 应截圆钢 | 锻造毛坯 | |
| 底面半径 | ||
| 高 | ||
| 体积 |
解得x=______cm.
解:(1)本题建立方程的相等关系是圆钢体积=毛坯体积.
(2)设截取直径为8cm的圆钢xcm,根据数量关系填表:
根据题意列方程:π×( )2×x=π×(
)2×x=π×(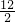 )2×8.
)2×8.
解得x=18.
故答案为:(1)圆钢体积=毛坯体积;(2)截取直径为8cm的圆钢xcm;π×( )2×x=π×(
)2×x=π×(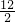 )2×8;18.
)2×8;18.
分析:根据已知本题建立方程的相等关系是圆钢体积=毛坯体积,进而表示出两者体积得出等式求出即可.
点评:此题主要考查了一元一次方程的应用,根据圆钢体积=毛坯体积得出是解题关键.
(2)设截取直径为8cm的圆钢xcm,根据数量关系填表:
| 应截圆钢 | 锻造毛坯 | |
| 底面半径 |  | 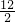 |
| 高 | x | 8 |
| 体积 | π×( )2×x )2×x | π×(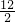 )2×8 )2×8 |
 )2×x=π×(
)2×x=π×(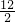 )2×8.
)2×8.解得x=18.
故答案为:(1)圆钢体积=毛坯体积;(2)截取直径为8cm的圆钢xcm;π×(
 )2×x=π×(
)2×x=π×(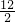 )2×8;18.
)2×8;18.分析:根据已知本题建立方程的相等关系是圆钢体积=毛坯体积,进而表示出两者体积得出等式求出即可.
点评:此题主要考查了一元一次方程的应用,根据圆钢体积=毛坯体积得出是解题关键.

练习册系列答案
相关题目