��Ŀ����
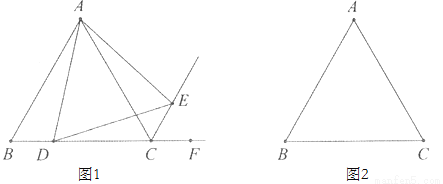
�����߶���ȵ������ν����ȱ������Σ����������Ƕ���60��. ��ABC�ǵȱ������Σ���D��BC����ֱ�����˶�������AD����AD����ֱ�ߵ��Ҳ�����DAE=60�㣬����ABC����ǡ�ACF�Ľ�ƽ��������ֱ���ڵ�E.
��1����ͼ1������D���߶�BC��ʱ���������AD��AE�Ĵ�С��ϵ��������֤����
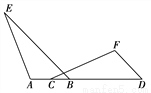
��2����ͼ2������D���߶�BC�ķ����ӳ�����ʱ���������ⲹȫͼ�Σ������������ۻ�������?��˵������.
��ϰ��ϵ�д�
�����Ŀ
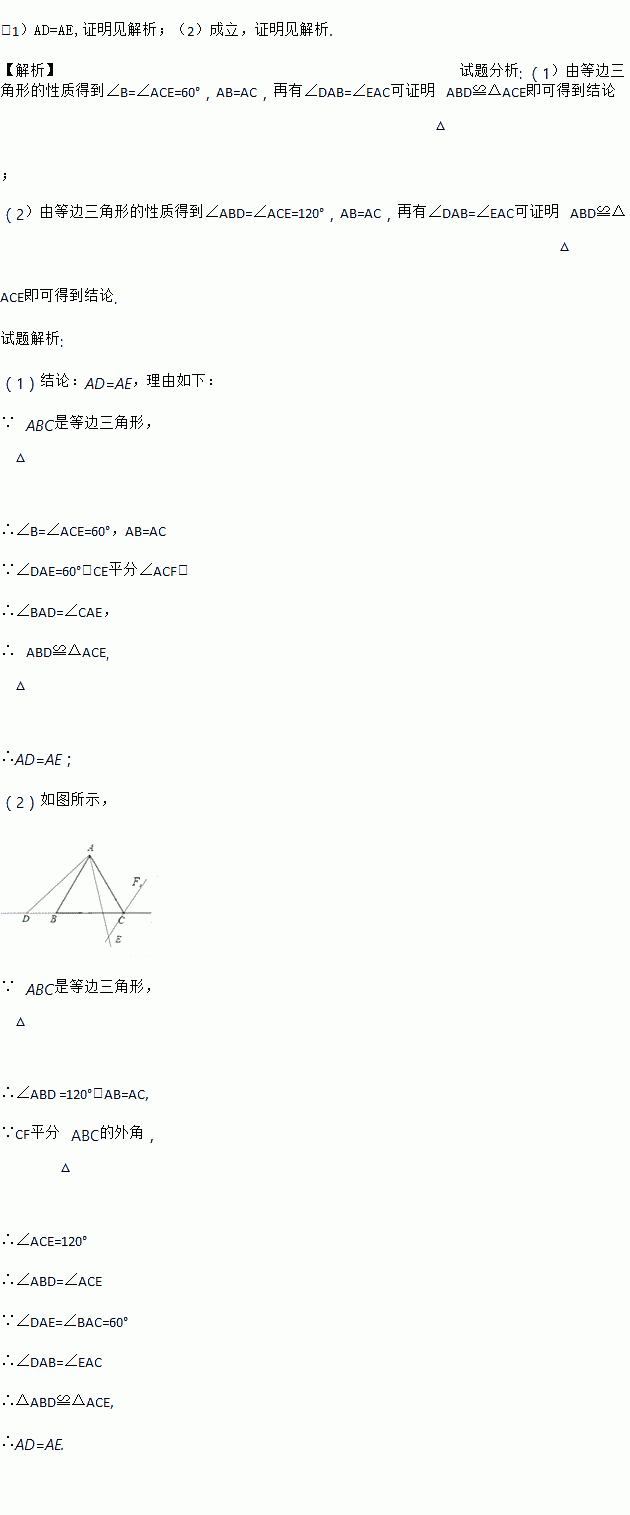

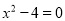 ��
��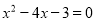 .
.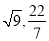 ,��,(
,��,( 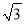 )0,������������(��)
)0,������������(��)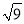 B.
B. 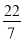 C. �� D. (
C. �� D. (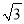 )0
)0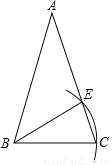
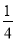 ��a��0 B. a��-
��a��0 B. a��-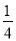 C. a��-
C. a��-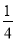 D. a��-
D. a��-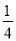 ��a��0
��a��0