题目内容
14．计算：（1）$\frac{a+2}{{a}^{2}-2a}$•$\frac{{a}^{2}-4a+4}{a+2}$；
（2）$\frac{x-2}{{x}^{2}-1}$÷$\frac{x+1}{{x}^{2}+2x+1}$．
分析 （1）原式约分即可得到结果；
（2）原式利用除法法则变形，约分即可得到结果．
解答 解：（1）原式=$\frac{a+2}{a（a-2）}$•$\frac{（a-2）^{2}}{a+2}$=$\frac{a-2}{a}$；
（2）原式=$\frac{x-2}{（x+1）（x-1）}$•$\frac{（x+1）^{2}}{x+1}$=$\frac{x-2}{x-1}$．
点评 此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
4．
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列，若规定（m、n）表示第m排从左向右第n个数，则（6，5）与（13，6）表示的两数之积是（ ）
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列，若规定（m、n）表示第m排从左向右第n个数，则（6，5）与（13，6）表示的两数之积是（ ）| A． | $\sqrt{6}$ | B． | 6 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
5．
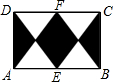如图，一个矩形区域ABCD，点E、F分别是AB、DC的中点，则一只蝴蝶落在阴影部分的概率是（ ）
如图，一个矩形区域ABCD，点E、F分别是AB、DC的中点，则一只蝴蝶落在阴影部分的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{17}{38}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{2}$ |
19．
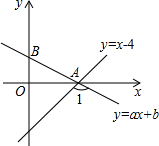如图，已知直线y=x-4与x轴交于点A，直线y=ax+b也经过点A，且与y轴的正半轴交于点B，若∠1=105°，则直线AB的解析式为（ ）
如图，已知直线y=x-4与x轴交于点A，直线y=ax+b也经过点A，且与y轴的正半轴交于点B，若∠1=105°，则直线AB的解析式为（ ）| A． | y=-$\frac{1}{2}$x+2 | B． | y=$\frac{1}{2}$x+2 | C． | y=$\frac{\sqrt{3}}{3}$x-$\frac{4\sqrt{3}}{3}$ | D． | y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$ |
3．
如图，在△ABC中，∠ACB=90°，DE垂直平分AB，垂足为D，如果∠A=30°，AB=6$\sqrt{3}$cm，那么CE等于（ ）
如图，在△ABC中，∠ACB=90°，DE垂直平分AB，垂足为D，如果∠A=30°，AB=6$\sqrt{3}$cm，那么CE等于（ ）| A． | 3cm | B． | 2cm | C． | 4cm | D． | $\sqrt{3}$cm |