题目内容
 如图,点A、B、C都在⊙O上,若∠BOC=72°,则∠C的度数为
如图,点A、B、C都在⊙O上,若∠BOC=72°,则∠C的度数为考点:圆周角定理
专题:探究型
分析:先根据圆周角定理求出∠A的度数,再由等腰三角形的性质即可得出结论.
解答:解:∵点A、B、C都在⊙O上,∠BOC=72°,
∴∠A=
∠BOC=
×72°=36°,
∵OA=OC,
∴∠C=∠A=36°.
故答案为:36°.
∴∠A=
| 1 |
| 2 |
| 1 |
| 2 |
∵OA=OC,
∴∠C=∠A=36°.
故答案为:36°.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知点(a,
)是y=kx与y=-
两函数图象的一个交点.则k=( )
| 3 |
| ||
| x |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
若关于x的二次函数y=x2-2mx+1的图象与端点在(-1,1)和(3,4)的线段只有一个交点,则m的值可能是( )
A、
| ||
B、-
| ||
C、
| ||
D、
|
如图,将四边形纸片ABCD沿着BD折叠,A点恰好落在BC上(BC>AB).再将四边形纸片ABCD的B点折向D,此时CB与CD恰好重合,得到折线CE.E点落在AD上,则下列结论正确的是( )


| A、AB∥CD |
| B、AD∥BC |
| C、∠ADB=∠BDC |
| D、∠ADB>∠BDC |
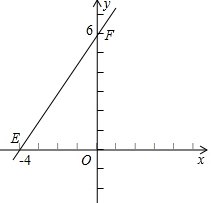 如图,直线l:y=kx+6分别于x轴,y轴交于E、F点,点E的坐标为(-4,0).若点A的坐标为(-3,0),点P(x,y)是平面内的一个动点.
如图,直线l:y=kx+6分别于x轴,y轴交于E、F点,点E的坐标为(-4,0).若点A的坐标为(-3,0),点P(x,y)是平面内的一个动点. 实践操作:
实践操作: