题目内容
 如图,长方形的纸片ABCD中,AB=8cm,把该纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=
如图,长方形的纸片ABCD中,AB=8cm,把该纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=| 25 |
| 4 |
考点:翻折变换(折叠问题)
专题:几何图形问题
分析:根据折叠可得∠1=∠2,然后再根据平行线的性质可得∠1=∠3,进而得到∠2=∠3,再根据等角对等边可得FC=AF=
cm,然后再利用勾股定理计算出AD.
| 25 |
| 4 |
解答: 解:根据折叠可得∠1=∠2,
解:根据折叠可得∠1=∠2,
∵AB∥DC,
∴∠1=∠3,
∴∠2=∠3,
∴FC=AF=
cm,
∵四边形ABCD是矩形,
∴∠D=90°,DC=AB=8cm,
∴DF=8-
=
cm,
∴AD=
=6cm.
 解:根据折叠可得∠1=∠2,
解:根据折叠可得∠1=∠2,∵AB∥DC,
∴∠1=∠3,
∴∠2=∠3,
∴FC=AF=
| 25 |
| 4 |
∵四边形ABCD是矩形,
∴∠D=90°,DC=AB=8cm,
∴DF=8-
| 25 |
| 4 |
| 7 |
| 4 |
∴AD=
| AF2-DF2 |
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为了筹办“经典红歌唱响金色校园”大合唱,学校选了四首经典红歌:
为了筹办“经典红歌唱响金色校园”大合唱,学校选了四首经典红歌:①《保卫黄河》;②《十送红军》;③《我们走在大路上》;④《我的祖国》.
班长对全班50名同学“你最想唱哪首歌”作了问卷调查,小明将班长的统计结果绘制成如图所示的统计图,并得出以下四个结论,其中错误的是( )
| A、最想唱《十送红军》的人最多 |
| B、最想唱《我的祖国》的人数是最想唱《我们走在大路上》的人数的3倍 |
| C、最想唱《保卫黄河》的人数占全班人数的20% |
| D、有10人对这4首红歌都不想唱 |
 如图,将△ABC绕着点O顺时针旋转90°后得到△A1B1C1,画出旋转后的△A1B1C1.
如图,将△ABC绕着点O顺时针旋转90°后得到△A1B1C1,画出旋转后的△A1B1C1. 如图,已知AD=BC,AB=DC,DE=BF,问:BE与DF是否相等?并说明为什么?
如图,已知AD=BC,AB=DC,DE=BF,问:BE与DF是否相等?并说明为什么? 如图为公园的一块草坪,其四角上各有一棵树,现园林工人想使这个草坪的面积扩大一倍,又要四棵树不动,并使扩大后的草坪为平行四边形,试问:这个想法能否实现?若能请你设计出草图?否则请说明理由.
如图为公园的一块草坪,其四角上各有一棵树,现园林工人想使这个草坪的面积扩大一倍,又要四棵树不动,并使扩大后的草坪为平行四边形,试问:这个想法能否实现?若能请你设计出草图?否则请说明理由.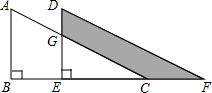 如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.设图中,AB=8,BE=5,GE=5,求图中阴影部分的面积.
如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.设图中,AB=8,BE=5,GE=5,求图中阴影部分的面积.