题目内容
15.用图象法解下列二元一次方程组:$\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$.分析 先利用描点法画出函数x+y=5和函数y=2x-1的图象,然后确定它们的交点坐标,再利用函数图象交点坐标为两函数解析式组成的方程组的解即可得到答案.
解答 解:如图:
直线x+y=5和直线y=2x-1的交点坐标为(2,3),
所以方程组$\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$;
点评 本题主要考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
5.二元一次方程x+2y=9的所有正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.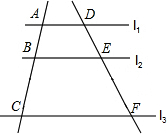 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和点D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和点D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,则EF的长是( )
 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和点D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和点D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,则EF的长是( )| A. | $\frac{18}{5}$ | B. | $\frac{48}{5}$ | C. | 10 | D. | 6 |
10.下列各式中不能用平方差公式进行因式分解的是( )
| A. | 1-a4 | B. | -16a2+b2 | C. | -m4-n4 | D. | 9a2-b4 |
7.一个正方体的截面不可能是( )
| A. | 三角形 | B. | 梯形 | C. | 五边形 | D. | 七边形 |