题目内容
8．解方程组：$\left\{\begin{array}{l}{5x+4y=24}\\{10x+2y=21}\end{array}\right.$．分析 方程组利用加减消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{5x+4y=24①}\\{10x+2y=21②}\end{array}\right.$，
②×2-①得：15x=18，即x=$\frac{6}{5}$，
把x=$\frac{6}{5}$代入①得：y=$\frac{9}{2}$，
则方程组的解为$\left\{\begin{array}{l}{x=\frac{6}{5}}\\{y=\frac{9}{2}}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
18．某公司生产的A种产品，它的成本是2元，售价是3元，年销售量是100万件，为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是x（十万元）时，产品的销售量将是原销售量的y倍，y与x的关系如下表：
（1）已知y与x之间满足我们学习过的三种函数（即一次函数、反比例函数、二次函数）关系中的一种，请求出y与x之间的函数关系式，不要求写出自变量的取值范围；
（2）如果把利润看做是销售总额减去成本费和广告费，试写出年利润S（十万元）与广告费x（十万元）的函数关系式；
（3）如果每年投入的广告费为10万元～20万元，公司获得的最大利润是多少？
| x（十万元） | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
（2）如果把利润看做是销售总额减去成本费和广告费，试写出年利润S（十万元）与广告费x（十万元）的函数关系式；
（3）如果每年投入的广告费为10万元～20万元，公司获得的最大利润是多少？
19．下列命题中正确的是（ ）
| A． | 对角线相等的四边形一定是平行四边形 | |
| B． | 一组对边平行，一组对角相等的四边形是平行四边形 | |
| C． | 四条边相等的四边形是正方形 | |
| D． | 菱形的对角线互相平分且相等 |
如图，在正方形ABCD中，E、F分别在BC和DC上，且BE=DF，求证：
在Rt△ABC中，∠ACB=90°，CD⊥AB于D，∠ACD=3∠BCD，E是AB的中点，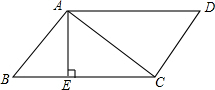
如图，在?ABCD中，AE⊥BC，垂足为E，且E为BC中点，若?ABCD的周长为20cm，△ABC的周长比?ABCD的周长少6cm，求?ABCD各边的长．