��Ŀ����
��֪������y=x2��2mx+m2��1��m�dz������Ķ���ΪP��ֱ��l��y=x��1��
��1����֤����P��ֱ��l�ϣ�
��2���������ߵĶԳ���Ϊx=��3��ֱ��д���������ߵĶ��������� ������x�ύ������Ϊ�� ����
��3���ڣ�2�������£��������ϵ㣨��2��b����ͼ���ϵĶԳƵ���������� ����
����4����3�� �������������������1�������䷽���õ�y=��x��m��2+m��1����P��m��m��1����Ȼ�����һ�κ���ͼ���ϵ�����������жϵ�P��ֱ��l�ϣ� ��2���ɣ�1����֪�����ߵĶԳ���Ϊx=m�������֪������ɵ�m=��3����������������ߵĶ������ꣻ��y=0����x�ύ������Ҳ������� ��3���ѵ㣨��2��b�����������߽���ʽ�����b��ֵ�������������ͼ���ϵĶԳƵ�����꣮ ...
��ϰ��ϵ�д�
�����Ŀ


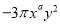 ��
��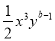 ���Ժϲ�����a+b=________.
���Ժϲ�����a+b=________.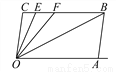
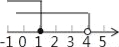
 �Ľ⼯�������ϱ�ʾ��ȷ���ǣ� ��
�Ľ⼯�������ϱ�ʾ��ȷ���ǣ� ��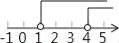 B��
B��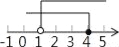
 D��
D��