题目内容
【题目】如图，已知
是正方形
内一点，以点
为旋转中心，将
按顺时针方向旋转使点
与点
重合，这时点旋转到
点．
设
的长为
，
的长为
，在图中用阴影标出旋转到
的过程中，边
所扫过区域的面积，并用含、
的式子表示它________；
若
，
，
，连接
，试猜想
的形状，并说明理由．
【答案】（1）
；（2）
是等腰直角三角形，理由见解析.
【解析】
（1）因为将△ABP按顺时针方向旋转使点A与点C重合，即旋转了90°，利用面积差可得边PA所扫过区域的面积=S=S扇形BAC+S△CBG-S△ABP-S扇形BPG，代入可得结论；
（2）先利用勾股定理得PG=
，根据勾股定理的逆定理可得：△PGC是等腰直角三角形．
（1）如图1，
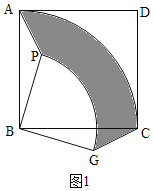
由旋转得：∠PBG=∠ABC=90°，BG=PB=b，
△ABP≌△CBG，
∴S=S扇形BAC+S△CBG-S△ABP-S扇形BPG，
=
，
=
，
故答案为：；
如图
，是等腰直角三角形，
理由是：∵
，
，
∴
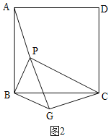
是等腰直角三角形，
∴
，
中，
，
，
∴
，
∴是直角三角形，
∵
，
∴是等腰直角三角形．
练习册系列答案
53随堂测系列答案
相关题目
