Question

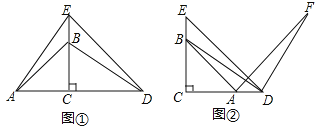
【题目】如图（1）所示，A，E，F，C在一条直线上，AE＝CF，过E，F分别作DE⊥AC，BF⊥AC，若AB＝CD，求证EG=FG.(提示：先证△ABF≌△CDE，得BF=DE，再证△BFG≌△DEG)；若将△DEC的边EC沿AC方向移动，变为图（2）时，其余条件不变，上述结论是否成立？请说明理由.

Answer 1

【答案】成立，证明详见解析

【解析】

结论仍然成立，先利用HL判定Rt△ABF≌Rt△CDE，得出BF=DE；再利用AAS判定△BFG≌△DEG，从而得出EG=FG.

解：结论仍然成立；

理由如下：

∵DE⊥AC，BF⊥AC，

∴∠DEF=∠BFE=90°．

∵AE=CF，

∴AEEF=CFEF．

即AF=CE．

在Rt△ABF和Rt△CDE中，

，

∴Rt△ABF≌Rt△CDE（HL），

∴BF=DE．

在△BFG和△DEG中，

，

∴△BFG≌△DEG（AAS），

∴EG=FG.