题目内容
 如图,直线l与x轴交于点P(1,0),与x轴所夹的锐角为θ,且tanθ=
如图,直线l与x轴交于点P(1,0),与x轴所夹的锐角为θ,且tanθ=| 3 |
| 2 |
| 1 |
| a |
(1)求B、D两点的坐标,并用含a的代数式表示b和c;
(2)①若关于x的方程x2+
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
②若抛物线y=
| 1 |
| a |
考点:二次函数综合题
专题:综合题,压轴题
分析:(1)作DE⊥x轴于E,BF⊥x轴于F,在Rt△PDE中,利用正切的定义得到tanθ=tan∠DPE=
=
,可求出DE=3,于是确定D点坐标为(3,3);在Rt△PBF中用同样方法可确定B点坐标为(-1,-3);再把B(-1,-3)、D(3,3)代入y=
x2+bx+c得方程组
,把它看作为关于b、c的方程组,解得b=
-
,c=-
-
;
(2)①根据根的判别式得到△=(
a)2-4(a2-
a+
)≥0,整理后得到(a-1)2≤0,根据非负数的性质得到a-1=0,即a=1,即可得到此时抛物线的解析式为y=x2-
x-
;
②利用抛物线与x轴两交点的距离公式得到AC=
=a
=
,把b=
-
,c=-
-
代入整理得到AC=
,而S四边形ABCD=S△ABC+S△ADC=
AC×3+
AC×3=3AC,则S四边形ABCD=
,由于a>0,9a2+64没有最大值,也没有最小值,即
,没有最大值,也没有最小值.
| DE |
| PE |
| 3 |
| 2 |
| 1 |
| a |
|
| 3 |
| 2 |
| 2 |
| a |
| 3 |
| 2 |
| 3 |
| a |
(2)①根据根的判别式得到△=(
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 9 |
| 2 |
②利用抛物线与x轴两交点的距离公式得到AC=
| ||||
|
|
b2-
|
| a2b2-4ac |
| 3 |
| 2 |
| 2 |
| a |
| 3 |
| 2 |
| 3 |
| a |
| 1 |
| 2 |
| 9a2+64 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9a2+64 |
| 9a2+64 |
解答:解:(1)作DE⊥x轴于E,BF⊥x轴于F,如图,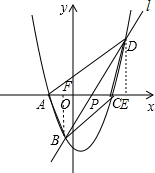
∵点P(1,0),tanθ=
,D(3,n),
∴OP=1,OE=3,
∴PE=2,
在Rt△PDE中,tanθ=tan∠DPE=
=
,
∴DE=3,
∴D点坐标为(3,3);
∵B点坐标(m,-3),
∴BF=3,
在Rt△PBF中,tanθ=tan∠FPB=
=
,
∴PF=2,
∴OF=1,
∴B点坐标为(-1,-3);
把B(-1,-3)、D(3,3)代入y=
x2+bx+c得
,
解得b=
-
,c=-
-
;
(2)①根据题意得△=(
a)2-4(a2-
a+
)≥0,
∴(a-1)2≤0,
∴a-1=0,即a=1,
∴此时抛物线的解析式为y=x2-
x-
;
②四边形ABCD的面积无最大值和最小值.理由如下:
AC=
=a
=
,
∵b=
-
,c=-
-
,
∴AC=
=
,
∵S四边形ABCD=S△ABC+S△ADC=
AC×3+
AC×3=3AC,
∴S四边形ABCD=
,
∵a>0,
∴9a2+64没有最大值,也没有最小值,即
,没有最大值,也没有最小值
∴四边形ABCD的面积无最大值和最小值.

∵点P(1,0),tanθ=
| 3 |
| 2 |
∴OP=1,OE=3,
∴PE=2,
在Rt△PDE中,tanθ=tan∠DPE=
| DE |
| PE |
| 3 |
| 2 |
∴DE=3,
∴D点坐标为(3,3);
∵B点坐标(m,-3),
∴BF=3,
在Rt△PBF中,tanθ=tan∠FPB=
| BF |
| PF |
| 3 |
| 2 |
∴PF=2,
∴OF=1,
∴B点坐标为(-1,-3);
把B(-1,-3)、D(3,3)代入y=
| 1 |
| a |
|
解得b=
| 3 |
| 2 |
| 2 |
| a |
| 3 |
| 2 |
| 3 |
| a |
(2)①根据题意得△=(
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
∴(a-1)2≤0,
∴a-1=0,即a=1,
∴此时抛物线的解析式为y=x2-
| 1 |
| 2 |
| 9 |
| 2 |
②四边形ABCD的面积无最大值和最小值.理由如下:
AC=
| ||||
|
|
b2-
|
| a2b2-4ac |
∵b=
| 3 |
| 2 |
| 2 |
| a |
| 3 |
| 2 |
| 3 |
| a |
∴AC=
a2(
|
| 1 |
| 2 |
| 9a2+64 |
∵S四边形ABCD=S△ABC+S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形ABCD=
| 3 |
| 2 |
| 9a2+64 |
∵a>0,
∴9a2+64没有最大值,也没有最小值,即
| 9a2+64 |
∴四边形ABCD的面积无最大值和最小值.
点评:本题考查了二次函数综合题:二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象为抛物线,其顶点式为y=a(x-
)2+
,当a>0,y最小值=
;当a<0,y最,大值=
;对于一元二次方程的根的判别式和三角函数的定义要熟练运用.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 4ac-b2 |
| 4a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
已知△ABC的三边长分别为9cm、14cm、13cm,分别以A、B、C三点为圆心作圆,使所作的三个圆两两外切,则其中最大圆的半径
为( )
为( )
| A、8cm | B、9cm |
| C、10cm | D、11cm |
 如图,小正方形方格的边长为1cm,则求图中扇形OAB的面积.
如图,小正方形方格的边长为1cm,则求图中扇形OAB的面积. 如图,OC是∠AOB的平分线,P是OC上一点,⊙P与OA相切于D,求证:OB与⊙P相切.
如图,OC是∠AOB的平分线,P是OC上一点,⊙P与OA相切于D,求证:OB与⊙P相切.


 ∵
∵ 如图AE∥BD,∠A=57°,∠BDE=125°,BC=4,BD=5.
如图AE∥BD,∠A=57°,∠BDE=125°,BC=4,BD=5.