题目内容
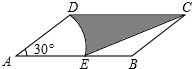 如图,在?ABCD中,AD=4,AB=8,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是
如图,在?ABCD中,AD=4,AB=8,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是考点:平行四边形的性质,扇形面积的计算
专题:
分析:过D点作DF⊥AB于点F.可求?ABCD和△BCE的高,观察图形可知阴影部分的面积=?ABCD的面积-扇形ADE的面积-△BCE的面积,计算即可求解.
解答:解: 过D点作DF⊥AB于点F.
过D点作DF⊥AB于点F.
∵AD=4,AB=8,∠A=30°,
∴DF=AD•sin30°=2,EB=AB-AE=4,
∴阴影部分的面积:8×2-
-4×2×
=16-
π-4
=12-
π.
故答案为:12-
π.
 过D点作DF⊥AB于点F.
过D点作DF⊥AB于点F.∵AD=4,AB=8,∠A=30°,
∴DF=AD•sin30°=2,EB=AB-AE=4,
∴阴影部分的面积:8×2-
| 30×π×42 |
| 360 |
| 1 |
| 2 |
=16-
| 4 |
| 3 |
=12-
| 4 |
| 3 |
故答案为:12-
| 4 |
| 3 |
点评:考查了平行四边形的性质,扇形面积的计算,本题的关键是理解阴影部分的面积=?ABCD的面积-扇形ADE的面积-△BCE的面积.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
下列实数中,无理数是( )
| A、0 | ||||
B、-
| ||||
C、
| ||||
D、
|
 如图,△ABC中,AC、BC上的中线交于点O,且BE⊥AD.若BD=5,BO=4,则AO的长为
如图,△ABC中,AC、BC上的中线交于点O,且BE⊥AD.若BD=5,BO=4,则AO的长为