题目内容
11.把抛物线y=-2x2-4x-3向右平移2个单位,再向上平移4个单位,求所得抛物线的关系式.分析 先将抛物线的解析式化为顶点式,然后根据平移规律平移即可得到解析式.
解答 解:y=-2x2-4x-3=-2(x+1)2-1,则该抛物线的顶点坐标是(-1,-1),
根据平移规律,右平移2个单位,再向上平移4个单位得到的抛物线的顶点坐标是:(1,3),
则平移后的抛物线的解析式为:y=-2(x-1)2+3=-2x2+4x+1,
即平移后抛物线的解析式为:y=-2(x-1)2+3或y=-2x2+4x+1.
点评 本题考查的是二次函数的图象与几何变换,熟知“上加下减,左加右减”的法则是解答此题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.以下不能构成三角形边长的数组是( )
| A. | 1,$\sqrt{5}$,2 | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 3,4,5 | D. | 32,42,52 |
6.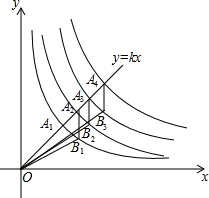 如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )
如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )
 如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )
如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )| A. | 1007 | B. | $\frac{2013}{2}$ | C. | 1006 | D. | $\frac{2011}{2}$ |
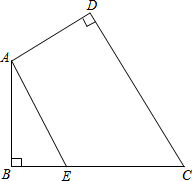 如图,四边形ABCD中,∠D=∠B=90°,∠AEC=∠BAD,求证:AE∥DC.
如图,四边形ABCD中,∠D=∠B=90°,∠AEC=∠BAD,求证:AE∥DC.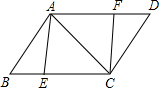 如图,已知点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF
如图,已知点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF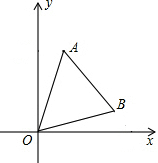 如图,平面直角坐标系中,A(1,4),B(3,1)
如图,平面直角坐标系中,A(1,4),B(3,1)