题目内容
6.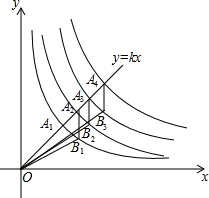 如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )
如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2014=$\frac{2014}{x}$的图象在第一象限内分别交于点A1,A2,…A2014.点B1,B2,…,B2013分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y2013=$\frac{2013}{x}$的图象上,且A2B1,A3B2,…,A2014B2013分别与y轴平行,连接OB1,OB2,…,OB2013,则△OA2B1,△OA3B2,…,△OA2014B2013的面积之和为( )| A. | 1007 | B. | $\frac{2013}{2}$ | C. | 1006 | D. | $\frac{2011}{2}$ |
分析 根据反比例函数$y=\frac{k}{x}$中k的几何意义,求得${S}_{△{{OA}_{2}B}_{1}}$=${S}_{{△A}_{2}OC}$-${S}_{△{OB}_{1}C}$=$\frac{1}{2}$×(2-1)=$\frac{1}{2}$,${S}_{△{{OA}_{3}B}_{2}}$=${S}_{{△A}_{3}OD}$-${S}_{{△B}_{2}OD}$=$\frac{1}{2}$×(3-2)=$\frac{1}{2}$,…${S}_{{{△OA}_{2014}B}_{2013}}$=$\frac{1}{2}$,得到△OA2B1,△OA3B2,…,△OA2014B2013的面积之和=2013×$\frac{1}{2}$=$\frac{2013}{2}$.
解答 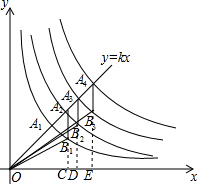 解:延长A2B1,A3B2,A4B3分别于x轴交于C,D,E,
解:延长A2B1,A3B2,A4B3分别于x轴交于C,D,E,
∵A2B1,A3B2,…,A2014B2013分别与y轴平行,
∴${S}_{△{{OA}_{2}B}_{1}}$=${S}_{{△A}_{2}OC}$-${S}_{△{OB}_{1}C}$=$\frac{1}{2}$×(2-1)=$\frac{1}{2}$,
${S}_{△{{OA}_{3}B}_{2}}$=${S}_{{△A}_{3}OD}$-${S}_{{△B}_{2}OD}$=$\frac{1}{2}$×(3-2)=$\frac{1}{2}$,
…
${S}_{{{△OA}_{2014}B}_{2013}}$=$\frac{1}{2}$,
∴△OA2B1,△OA3B2,…,△OA2014B2013的面积之和=2013×$\frac{1}{2}$=$\frac{2013}{2}$.
故答案为:$\frac{2013}{2}$.
点评 本题主要考查了待定系数法求反比例函数与一次函数的解析式和反比例函数$y=\frac{k}{x}$中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

| A. | 直线x=1 | B. | 直线x=-1 | C. | 直线x=-2 | D. | 直线x=$\frac{1}{2}$ |
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
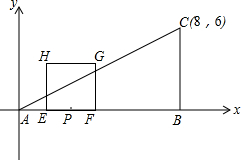 在Rt△ABC中,∠ABC=90°,以A为坐标原点,AB所在直线为x轴,建立平面直角坐标,且C坐标(8,6),点P在AB上,AP=2,E、F同时从点P出发,分别沿PA、PB以每秒1个单位的速度向A、B匀速运动,点E到达A后立即以原速沿AB向B运动,点E再次返回点P停止,点F也随之停止运动,在点E、F运动过程中,以EF为边向上做正方形EFGH,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠面积为S.
在Rt△ABC中,∠ABC=90°,以A为坐标原点,AB所在直线为x轴,建立平面直角坐标,且C坐标(8,6),点P在AB上,AP=2,E、F同时从点P出发,分别沿PA、PB以每秒1个单位的速度向A、B匀速运动,点E到达A后立即以原速沿AB向B运动,点E再次返回点P停止,点F也随之停止运动,在点E、F运动过程中,以EF为边向上做正方形EFGH,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠面积为S.

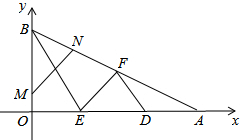 如图,在平面直角坐标系中,Rt△ABO的顶点A、B的坐标分别为(3,0)、(0,1),点D、E是AO的三等分点,且点D在点E的右侧,点F是AB的中点.动点P从点B出发,以每秒$\sqrt{2}$个单位长度的速度沿折线BE-EF-FD运动.当点P不与点E、F重合时,过点P作其运动所在线段的垂线,交AB边于点N,交BO或AO于点M.设点P运动时间为t(秒).
如图,在平面直角坐标系中,Rt△ABO的顶点A、B的坐标分别为(3,0)、(0,1),点D、E是AO的三等分点,且点D在点E的右侧,点F是AB的中点.动点P从点B出发,以每秒$\sqrt{2}$个单位长度的速度沿折线BE-EF-FD运动.当点P不与点E、F重合时,过点P作其运动所在线段的垂线,交AB边于点N,交BO或AO于点M.设点P运动时间为t(秒).