题目内容
17．若关于x、y的二元一次方程组$\left\{\begin{array}{l}{3x+y=1+a}\\{x+3y=3}\end{array}\right.$的解满足x-y=2，则常数a的值为6．分析 把a当作已知数，解方程组求出x、y的值，代入x-y=2得出方程，求出方程的解即可．
解答 解：$\left\{\begin{array}{l}{3x+y=1+a①}\\{x+3y=3②}\end{array}\right.$，
①-②得：2x-2y=a-2，
把x-y=2代入2x-2y=a-2中，
解得：a=6．
故答案为：6．
点评 本题考查了二元一次方程组的解，解二元一次方程组，解一元一次方程的应用，关键是能根据题意得出关于a的方程．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
已知：如图，在△ABC中，AD平分∠BAC，EF垂直平分AD．求证：∠B=∠CAF．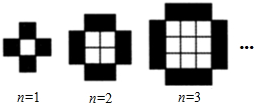
当白色小正方形个数n等于1，2，3，…时，由白色小正方形和黑色小正方形组成的图形分别如图所示，则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n（用n表示，n是正整数）．