题目内容

16．观察下列算式：32=9，33=27，34=81，35=243，…，那么32016的末位数字为（　　）
A．1B．3C．7D．9

分析 从运算的结果可以看出尾数以3、9、7、1四个数字一循环，用2016除以4，余数是几就和第几个数字相同，由此解决问题即可．

解答 解：已知31=3，末位数字为3，
32=9，末位数字为9，
33=27，末位数字为7，
34=81，末位数字为1，
35=243，末位数字为3，
36=729，末位数字为9，
37=2187，末位数字为7，
38=6561，末位数字为1，
…
由此得到：3的1，2，3，4，5，6，7，8，…次幂的末位数字以3、9、7、1四个数字为一循环，
又∵2016÷4=504，
∴32016的末位数字与34的末位数字相同是1．
故选A．

点评 此题考查尾数特征及规律型：数字的变化类，通过观察得出3的乘方的末位数字以3、9、7、1四个数字为一循环是解决问题的关键．

练习册系列答案
相关题目
6．观察下面的变形规律：$\frac{1}{1×2}=1-\frac{1}{2}$；$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$；$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$；…；根据这个规律计算：$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+$…$+\frac{1}{n×（n+1）}$=$\frac{n}{n+1}$．
7．如图，在数轴上点M表示的数可能是（　　）
A．1.5B．-1.5C．-2.5D．2.5
4．已知五边形ANCDE∽五边形A1B1C1D1E1，五边形ABCDE的最短边为2，最长边为6，五边形A1B1C1D1E1，的最长边是12，则五边形A1B1C1D1E1的最短边是（　　）
A．4B．5C．6D．8
11．如图，菱形ABCD中，对角线AC，BD相交于点O，不添加任何辅助线，要使四边形ABCD是正方形，则需要添加一个条件是∠ABC=90°．（填一个即可）
1．某超市今年七月份的利润为40万元，九月份的利润为48.4万元，则八，九月份利润的平均增长率为10%．
8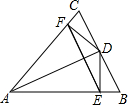．如图，在△ABC中，AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E，F分别为垂足，则下列四个结论：（1）∠DEF=∠DFE；（2）AE=AF；（3）AD平分∠EDF；（4）AD垂直平分EF．其中正确的有（　　）
A．1个B．2个C．3个D．4个
5．关于x的一元二次方程（m+2）x2+3x+m2=4的一根是0，则m的值是（　　）
A．2B．-2C．2或-2D．0
6．一个数的相反数是-2017，则这个数是（　　）
A．2017B．-2017C．$\frac{1}{2017}$D．-$\frac{1}{2017}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网