题目内容
11.如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
分析 (1)首先根据题意结合概率公式可得答案;
(2)首先根据(1)求得摸出两张牌面图形都是轴对称图形的有16种情况,若摸出两张牌面图形都是中心对称图形的有12种情况,继而求得小明赢与小亮赢的概率,比较概率的大小,即可知这个游戏是否公平.
解答 解:(1)共有4张牌,正面是中心对称图形的情况有3种,所以摸到正面是中心对称图形的纸牌的概率是$\frac{3}{4}$;
(2)列表得:
| A | B | C | D | |
| A | (A,B) | (A,C) | (A,D) | |
| B | (B,A) | (B,C) | (B,D) | |
| C | (C,A) | (C,B) | (C,D) | |
| D | (D,A) | (D,B) | (D,C) |
∴P(两张都是轴对称图形)=$\frac{1}{2}$,因此这个游戏公平.
点评 本题考查的是游戏公平性的判断,以及概率.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
1.下列图形是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2. 如图,已知直线AB、CD被直线AE所截,AB∥CD,∠1=60°,∠2的度数是( )
如图,已知直线AB、CD被直线AE所截,AB∥CD,∠1=60°,∠2的度数是( )
 如图,已知直线AB、CD被直线AE所截,AB∥CD,∠1=60°,∠2的度数是( )
如图,已知直线AB、CD被直线AE所截,AB∥CD,∠1=60°,∠2的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
19.-5的相反数是( )
| A. | -5 | B. | ±5 | C. | $\frac{1}{5}$ | D. | 5 |
2.如图,随着棋子摆放层数n的增加,棋子的个数y也在变化:

(1)填写表;
(2)对于给定的一个层数n,棋子的个数y是确定的吗?如果确定,请你写出y与n的函数关系式;如果不确定,说明理由.

(1)填写表;
| 层数n | 1 | 2 | 3 | 4 | 5 | 6 |
| 个数y | 1 | 3 | 5 | 7 | 9 | 11 |
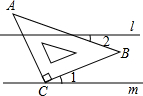 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为25度.
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为25度.