题目内容
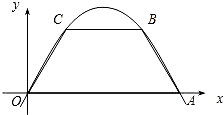 如图,在等腰梯形OABC中,CB∥OA,∠COA=60°BC=2,OA=4,且与x轴重合.
如图,在等腰梯形OABC中,CB∥OA,∠COA=60°BC=2,OA=4,且与x轴重合.(1)直接写出点A、B、C的坐标;
(2)求经过点O、A、B的抛物线解析式,并判断点C是否在抛物线上;
(3)在抛物线的OCB段,是否存在一点P(不与O、B重合),使得四边形OABP的面积最大?若存在,求出此时P点的坐标;若不存在,请说明理由.
分析:(1)A点坐标可根据OA的长获得;过B作BM⊥OA于M,利用等腰梯形的对称性可求得AM的长,已知∠COA=∠BAO=60°,即可求得BM的长,从而得到B、C的坐标.
(2)已知了抛物线图象上的三点坐标,可利用待定系数法求得该抛物线的解析式,然后将点C的坐标代入抛物线中进行验证即可.
(3)连接OB,易求得直线OB的解析式;过P作直线PD⊥x轴,交OB于D,设出点P的横坐标,根据抛物线和直线OB的解析式,可表示出P、D的纵坐标,即可得到PD的长;由于四边形OPBA中,△ABO的面积是定值,所以当四边形OPBA的面积最大时,△OBP的面积最大,此时PD的值最大,可根据得到的关于PD和P点横坐标的函数关系式,求得PD的最大值及对应的P点坐标.
(2)已知了抛物线图象上的三点坐标,可利用待定系数法求得该抛物线的解析式,然后将点C的坐标代入抛物线中进行验证即可.
(3)连接OB,易求得直线OB的解析式;过P作直线PD⊥x轴,交OB于D,设出点P的横坐标,根据抛物线和直线OB的解析式,可表示出P、D的纵坐标,即可得到PD的长;由于四边形OPBA中,△ABO的面积是定值,所以当四边形OPBA的面积最大时,△OBP的面积最大,此时PD的值最大,可根据得到的关于PD和P点横坐标的函数关系式,求得PD的最大值及对应的P点坐标.
解答: 解:(1)过B作BM⊥OA于M,则AM=1;
解:(1)过B作BM⊥OA于M,则AM=1;
在Rt△BMA中,AM=1,∠BAM=∠COA=60°,
∴BM=
AM=
,OM=4-AM=3;
∴B(3,
),
同理得C(1,
);
故:A(4,0),B(3,
),C(1,
).
(2)依题意设y=ax(x-4),又B(3,
)在该函数图象上,
∴-3a=
,
解得:a=-
,
∴y=-
x2+
x;
当x=1时,y=
,
故点C(1,
)在该函数图象上.

(3)如图,
连接OB,在抛物线上取点P,过P作PD⊥x轴,交OB于D,连接OP、BP;
则过OB的直线的解析式为y=
x,
∵S△OAB为定值,
∴使S△OPB最大,则四边形OPBA的面积最大;
∵PD=yP-yD=-
x2+
x-
x=-
x2+
x=-
(x-
)2+
,
∴当x=
时,PD最大,
将x=
代入y=-
x2+
x中,
得y=
;
此时P点的坐标为P(
,
).
 解:(1)过B作BM⊥OA于M,则AM=1;
解:(1)过B作BM⊥OA于M,则AM=1;在Rt△BMA中,AM=1,∠BAM=∠COA=60°,
∴BM=
| 3 |
| 3 |
∴B(3,
| 3 |
同理得C(1,
| 3 |
故:A(4,0),B(3,
| 3 |
| 3 |
(2)依题意设y=ax(x-4),又B(3,
| 3 |
∴-3a=
| 3 |
解得:a=-
| ||
| 3 |
∴y=-
| ||
| 3 |
4
| ||
| 3 |
当x=1时,y=
| 3 |
故点C(1,
| 3 |

(3)如图,
连接OB,在抛物线上取点P,过P作PD⊥x轴,交OB于D,连接OP、BP;
则过OB的直线的解析式为y=
| ||
| 3 |
∵S△OAB为定值,
∴使S△OPB最大,则四边形OPBA的面积最大;
∵PD=yP-yD=-
| ||
| 3 |
4
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 2 |
3
| ||
| 4 |
∴当x=
| 3 |
| 2 |
将x=
| 3 |
| 2 |
| ||
| 3 |
4
| ||
| 3 |
得y=
5
| ||
| 4 |
此时P点的坐标为P(
| 3 |
| 2 |
5
| ||
| 4 |
点评:此题主要考查了等腰梯形的性质、直角三角形的性质、二次函数解析式的确定、函数图象上点的坐标意义以及图形面积的求法等重要知识;类似于(3)题求面积最大(小)值问题,通常转化为二次函数的最值问题来解.

练习册系列答案
相关题目
 9、如图,在等腰梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,以下四个结论:①∠ABC=∠DCB,②OA=OD,③∠BCD=∠BDC,④S△AOB=S△DOC.
9、如图,在等腰梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,以下四个结论:①∠ABC=∠DCB,②OA=OD,③∠BCD=∠BDC,④S△AOB=S△DOC. 标系xoy,已知已知A(2,2
标系xoy,已知已知A(2,2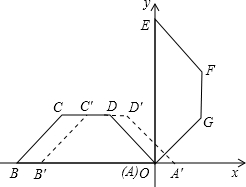
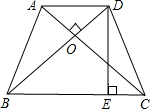 如图,在等腰梯形ABCD中,AD∥BC,AC⊥BD垂足为O,过点D作DE⊥BC于E,以下五个结论:①∠ABC=∠DCB;②OA=OD;③∠BCD=∠BDC;④S△AOB=S△DOC;⑤DE=
如图,在等腰梯形ABCD中,AD∥BC,AC⊥BD垂足为O,过点D作DE⊥BC于E,以下五个结论:①∠ABC=∠DCB;②OA=OD;③∠BCD=∠BDC;④S△AOB=S△DOC;⑤DE=