Question

如图，在等腰梯形ABCD中，AB‖CD，已知AB=6，BC=2

2

，∠DAB=45°，以AB所在直线为x轴，A为坐标原点，建立直角坐标系，将等腰梯形ABCD绕A点按顺时针方向旋转90°得到等腰梯形OEFG（O、E、F、G分别是A、B、C、D旋转后的对应点）（如图）．
（1）在直线DC上是否存在一点P，使△EFP为等腰三角形，若存在，写出P点的坐标，若不存在，请说明理由；
（2）将等腰梯形ABCD沿x轴的正半轴平行移动，设移动后的OA=x（0＜x≤6），等腰梯形ABCD与等腰梯形OEFG重叠部分的面积为y，求y与x之间的函数关系式．

Answer 1

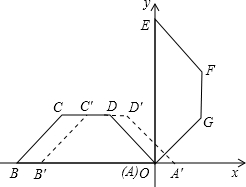
分析：（1）易得D（-2，2），△EFP为等腰三角形，应分情况进行探讨．EP=FP时，作出EF的垂直平分线，易得点P的坐标和D坐标重合为（-2，2），EP=EF时，与直线CD无交点，舍去这种情况，EF=FP时，可得P坐标为CD与y轴的交点为（0，2）；
（2）易得F（2，4），G（2，2），作出等腰梯形的两条高，得到等腰梯形是上底为2，高为2．当移动距离为0-2时，重合部分是三角形，底边为x，高为0.5x，易得面积；移动距离为2-4时，重合部分是四边形，可让梯形面积减去直角三角形面积；移动距离为4-6时，重合部分是三角形，易求得高与底边．

解答：解：（1）①EP=FP时，易求出D（-2，2），E（0，6），F（2，4），
由勾股定理得：DE²=（0+2）²+（6-2）²=20，DF²=（2+2）²+（4-2）²=20，
∴DE=DF，
即D在EF的垂直平分线上，
即作出EF的垂直平分线，易得点P的坐标和D坐标重合为（-2，2），
②EP=EF时，与直线CD无交点，舍去这种情况；
EF=FP时，可得P坐标为CD与y轴的交点为（0，2）
∴P（-2，2），P（0，2）；（1分）

（2）①当0＜x≤2时，重合部分是一小等腰直角三角形，底边长为x，高为0.5x，
∴y=

1

4

x²．（2分）
②当2≤x≤4时；重合部分是四边形，所在的梯形的上底为x-2，下底为x，高为2，三角形的底边为x，高为0.5x．
∴y=-

1

4

x²+2x-2．（2分）
③当4≤x≤6时；重合部分是梯形．
∴y=-

1

2

x²+4x-6．（2分）

点评：使△DFP为等腰三角形，应利用尺规作图得到相应的在直线CD上的点；运动过程中的面积应注意不同时期的不同状态，注意利用容易算出的面积表示．