题目内容
 如图,已知:△ABC、△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,两条直角边AB、AD重合,把AD绕点A逆时针旋转α角(0°<α<90°),到如图所示的位置时,BC分别与AD、AE相交于点F、G,则图中
如图,已知:△ABC、△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,两条直角边AB、AD重合,把AD绕点A逆时针旋转α角(0°<α<90°),到如图所示的位置时,BC分别与AD、AE相交于点F、G,则图中共有( )对相似三角形.
| A、1 | B、2 | C、3 | D、4 |
考点:相似三角形的判定
专题:
分析:根据已知及相似三角形的判定方法进行分析,从而得到答案.
解答:解:∵△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠EDA=90°,
∴∠C=∠B=∠DAE=∠E=45°,
∵∠CFA=∠B+∠FAB,∠GAB=∠FAG+∠FAB,
∴∠CFA=∠BAG,
∴△CAF∽△BGA,
∴△BGA∽△AGF∽△CAF;
还有△ABC≌△DEA,
∴相似三角形共有4对.
故选:D.
∴∠C=∠B=∠DAE=∠E=45°,
∵∠CFA=∠B+∠FAB,∠GAB=∠FAG+∠FAB,
∴∠CFA=∠BAG,
∴△CAF∽△BGA,
∴△BGA∽△AGF∽△CAF;
还有△ABC≌△DEA,
∴相似三角形共有4对.
故选:D.
点评:本题考查了相似三角形的判定:①有两个对应角相等的三角形相;②有两个对应边的比相等,且其夹角相等,则两个三角形相似;③三组对应边的比相等,则两个三角形相似.

练习册系列答案
相关题目
针对动物园中四种可爱的动物:熊猫、孔雀、小猴、梅花鹿,想了解本班同学喜欢哪种动物的人最多,则调查对象是( )
| A、本班全体同学 |
| B、熊猫、孔雀、小猴、梅花鹿 |
| C、记录下来的数据 |
| D、同学们的选票 |
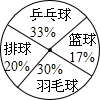 某班学生最喜欢的体育活动如图所示,则下列说法:①最喜欢乒乓球的人数占班级总人数的
某班学生最喜欢的体育活动如图所示,则下列说法:①最喜欢乒乓球的人数占班级总人数的| 33 |
| 100 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 17 |
| A、①② | B、①③④ |
| C、②③ | D、①②③ |
 有两所初级中学A校和B校,在校学生均为1000人.现根据两个统计图(如图1所示)得到以下统计结果:①A校男生比女生多20人;②B校男生比女生少60人;③两校合起来,则女生比男生多10人;④A校男生比B校男生多50人.其中正确的为( )
有两所初级中学A校和B校,在校学生均为1000人.现根据两个统计图(如图1所示)得到以下统计结果:①A校男生比女生多20人;②B校男生比女生少60人;③两校合起来,则女生比男生多10人;④A校男生比B校男生多50人.其中正确的为( )| A、①③ | B、②④ | C、②③ | D、①④ |
 如图,点A,B,C都在直线a上,下列说法错误的是( )
如图,点A,B,C都在直线a上,下列说法错误的是( )| A、点A在射线BC上 |
| B、点C在直线AB上 |
| C、点A在线段BC上 |
| D、点C在射线AB上 |
已知:m是
的小数部分,则
的值( )
| 2 |
m2+
|
A、等于2
| ||
| B、等于0 | ||
| C、等于2 | ||
| D、随m的变化而变化 |