题目内容
9.将乘法公式适当变形使用,有时可以给解题带来意想不到的帮助.比如我们可以将完全平方公式进行如下变形:①a2+b2=$\frac{(a+b)^{2}+(a-b)^{2}}{2}$;
②ab=$\frac{1}{4}$(a+b)2-$\frac{1}{4}$(a-b)2.
试用以上变形解决下面的问题:
已知自然数a和b,a+b=40.
(1)求a2+b2的最小值;
(2)求ab的最大值.
分析 (1)根据题意表示出a、b的关系,根据配方法和非负数的性质解答即可;
(2)根据题意表示出a、b的关系,根据配方法和非负数的性质解答即可.
解答 解:(1)∵a+b=40,
∴b=40-a,
∴a2+b2=2a2-80a+1600
=2(a-20)2+800,
∴a2+b2的最小值是800;
(2)ab=a(40-a)
=40a-a2
=-(a-20)2+400,
∴ab的最大值是400.
点评 本题考查的是配方法的应用,正确运用配方法把代数式进行变形是解题的关键,注意完全平方的非负性的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知AD是△ABC的角平分线,四边形MBEF是平行四边形.求证:AF=BM.
如图,已知AD是△ABC的角平分线,四边形MBEF是平行四边形.求证:AF=BM.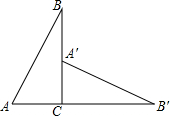 如图所示在△ABC中,∠ACB=90°,△CA′B′是由△ABC绕顶点C旋转得到的,且A,C,B′三点在同一直线上,那么A′B′与AB的关系怎样?试说明理由.
如图所示在△ABC中,∠ACB=90°,△CA′B′是由△ABC绕顶点C旋转得到的,且A,C,B′三点在同一直线上,那么A′B′与AB的关系怎样?试说明理由.