题目内容
3. 如图,直线AB,CD,EF被直线BF所截,∠B+∠1=180°,∠2=∠3.求证:∠B+∠F=180°.
如图,直线AB,CD,EF被直线BF所截,∠B+∠1=180°,∠2=∠3.求证:∠B+∠F=180°.
分析 根据平行线的判定得出AB∥CD,CD∥EF,求出AB∥EF,根据平行线的性质得出即可.
解答 证明:∵∠B+∠1=180°,
∴AB∥CD,
∵∠2=∠3,
∴CD∥EF,
∴AB∥EF,
∴∠B+∠F=180°.
点评 本题考查了平行线的性质和判定的应用,能运用定理进行推理是解此题的关键,难度适中.

练习册系列答案
相关题目
14.下列分式一定有意义的是( )
| A. | $\frac{{x}^{2}+1}{{x}^{2}-1}$ | B. | $\frac{x+1}{x^2}$ | C. | $\frac{x-1}{{x}^{2}+1}$ | D. | $\frac{{x}^{2}}{x+1}$ |
11.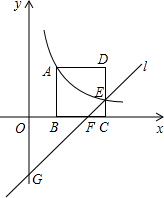 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),过点E的直线交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )| A. | ($\frac{5}{4}$,0) | B. | ($\frac{7}{4}$,0) | C. | ($\frac{9}{4}$,0) | D. | ($\frac{11}{4}$,0) |
18.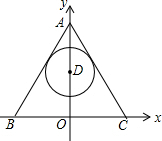 如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
 如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{3}$或3$\sqrt{3}$ | D. | 2$\sqrt{3}$或3$\sqrt{3}$ |
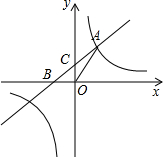 如图,直线y=x+b与双曲线y=$\frac{m}{x}$都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
如图,直线y=x+b与双曲线y=$\frac{m}{x}$都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.



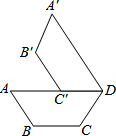 如图,在梯形ABCD中,AD∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于60度.
如图,在梯形ABCD中,AD∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于60度.