题目内容
12.不等式组$\left\{\begin{array}{l}{2x-4>0}\\{3(x-1)≤4x}\end{array}\right.$的解集是-3≤x<2.分析 先分别解两个不等式得到x>2和x≥-3,然后根据大小小大中间找确定不等式组的解集.
解答 解:$\left\{\begin{array}{l}{2x-4>0①}\\{3(x-1)≤4x②}\end{array}\right.$,
解①得x>2,
解②得x≥-3,
所以不等式组的解集为-3≤x<2.
故答案为-3≤x<2.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知一次函数y=kx+b(k≠0)的y随x的增大而增大,则下列结论中一定正确的是( )
| A. | k<0 | B. | k>0 | C. | b<0 | D. | b>0 |
 如图,PA、PB分别切⊙O于点A、B,∠P=80°,则∠C=50°.
如图,PA、PB分别切⊙O于点A、B,∠P=80°,则∠C=50°. 如图,直线AB,CD,EF被直线BF所截,∠B+∠1=180°,∠2=∠3.求证:∠B+∠F=180°.
如图,直线AB,CD,EF被直线BF所截,∠B+∠1=180°,∠2=∠3.求证:∠B+∠F=180°.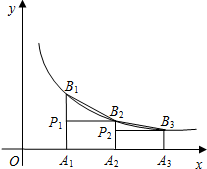 如图,已知点A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=$\frac{1}{x}$(x>0)的图象于点B1,B2,B3,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn,则S1+S2+S2+…+S2015=$\frac{2015}{4032}$.
如图,已知点A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=$\frac{1}{x}$(x>0)的图象于点B1,B2,B3,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn,则S1+S2+S2+…+S2015=$\frac{2015}{4032}$. 如图是每个画上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是( )
如图是每个画上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是( )