题目内容
3.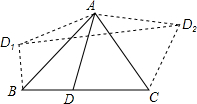 如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2$\sqrt{3}$+2,D是BC边上异于B、C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是9+4$\sqrt{3}$.
如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2$\sqrt{3}$+2,D是BC边上异于B、C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是9+4$\sqrt{3}$.
分析 如图所示:过点D2作D2E⊥BC,垂足为E.设DC=x,则BD=2$\sqrt{3}+2$-x.然后根据四边形D1BCD2的面积等于梯形D1BED2的面积减去三角形CED2的面积列函数关系是求解即可.
解答 解:如图所示:过点D2作D2E⊥BC,垂足为E.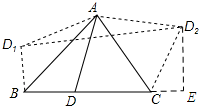
设DC=x,则BD=2$\sqrt{3}+2$-x.
由翻折的性质可知:∠D1BD=90°,∠ECD2=60°,D1B=BD=2$\sqrt{3}+2$-x,CD2=DC=x.
∵在Rt△CED2中,∠ECD2=60°
∴EC=$\frac{1}{2}x$,D2E=$\frac{\sqrt{3}}{2}x$.
∴${S}_{{D}_{1}BC{D}_{2}}$=${S}_{{D}_{1}BE{D}_{2}}$-${S}_{△CE{D}_{2}}$
=$\frac{1}{2}$(D1B+D2E)•BE-$\frac{1}{2}×CE×E{D}_{2}$
=$\frac{1}{2}×$(2$\sqrt{3}$+2-x+$\frac{\sqrt{3}}{2}x$)(2$\sqrt{3}$+2+$\frac{1}{2}x$)-$\frac{1}{2}×\frac{1}{2}x×\frac{\sqrt{3}}{2}x$
=$-\frac{1}{4}$(x-2)2+9+4$\sqrt{3}$.
∴当x=2时,四边形D1BCD2的面积有最大值,最大值为9+4$\sqrt{3}$.
故答案为:9+4$\sqrt{3}$.
点评 本题主要考查的是翻折的性质、二次函数的综合应用,根据题意列出函数关系式是解题的关键.

练习册系列答案
相关题目
9.某药品原价每盒25元,在国家的医改政策的指导下,连续两次降价a%,后售价为每盒18元,下列方程正确的是( )
| A. | 25(1+a%)2=18 | B. | 25(1-a%)2=18 | C. | 25(1-2a%)=18 | D. | 25(1-a2%)=18 |
10.下列各组数中不能作为直角三角形的三边长的是( )
| A. | 6,8,10 | B. | 7,24,25 | C. | 1.5,2,3 | D. | 9,12,15 |
 是方程
是方程 的两根,则
的两根,则 的值是( )
的值是( ) D.
D. 
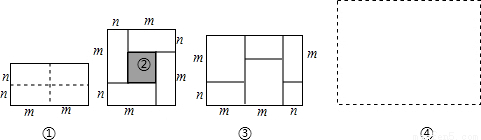
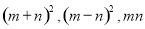 之间的等量关系.
之间的等量关系. 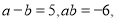 则
则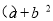 =
= 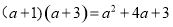 ,请你在图④中画出一个相应的几何图形。
,请你在图④中画出一个相应的几何图形。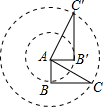 如图,Rt△ABC中,AC=$\sqrt{5}$,以点A为中心逆时针旋转90°得到Rt△AB′C′,则Rt△A′B′C′,则$\widehat{CC′}$的长为$\frac{\sqrt{5}}{2}$π.
如图,Rt△ABC中,AC=$\sqrt{5}$,以点A为中心逆时针旋转90°得到Rt△AB′C′,则Rt△A′B′C′,则$\widehat{CC′}$的长为$\frac{\sqrt{5}}{2}$π. 如图,正六边形ABCDEF的每一个外角的度数是60度.
如图,正六边形ABCDEF的每一个外角的度数是60度.