题目内容
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 是整数).
是整数).
⑴.求证:方程有两个不相等的实数根;
⑵.若方程的两个实数根分别为![]() (其中
(其中![]() ),设
),设![]() ,判断
,判断![]() 是否为变量
是否为变量![]() 的函数?如果是,请写出函数表达式;若不是,请说明理由.
的函数?如果是,请写出函数表达式;若不是,请说明理由.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)计算出判别式△的值,根据判别式的值即可判定方程有两个不相等的实数根;(2)解出关于![]() 的方程得到方程的两个实数根分别为
的方程得到方程的两个实数根分别为![]() (其中
(其中![]() )(根实际上是含
)(根实际上是含![]() 的代数式表示的)代入
的代数式表示的)代入![]() ,然后利用函数的定义进行判断即可.
,然后利用函数的定义进行判断即可.
试题解析:
⑴.证明:
∵方程 ![]() 关于
关于![]() 的一元二次方程,
的一元二次方程,
∴![]() ,△ =
,△ = ![]()
∵![]() 是整数 ∴
是整数 ∴![]() ∴
∴![]()
∴△ =![]()
∴方程有两个不相等的实数根.
⑵. ![]() 是变量
是变量![]() 的函数.理由如下:
的函数.理由如下:
解方程: 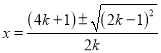 , ∴
, ∴![]() 或
或 ![]() ,
,
∵![]() 是整数, ∴
是整数, ∴![]() , ∴
, ∴![]() ,
,
∵![]() ∴
∴![]() ,
, ![]() . /span>
. /span>
∴![]() ,
,
∴![]() 是变量
是变量![]() 的函数.
的函数.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目