Question

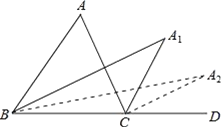
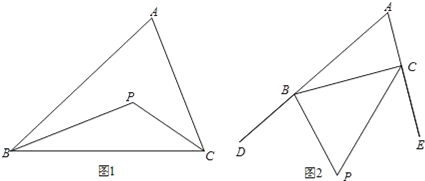
【题目】如图1，△ABC中，∠ABC与∠ACB的平分线交于点P，根据下列条件，求∠BPC的度数．

（1）若∠A=50°，则∠BPC=　　；

（2）从上述计算中，我们能发现：∠BPC=　　（用∠A表示）；

（3）如图2，若BP，CP分别是∠ABC与∠ACB的外角平分线，交于点P，则∠BPC=　　．（用∠A表示），并说明理由．

Answer 1

【答案】（1）∠BPC=115°；（2）90°∠A；（3）∠BPC=90°﹣∠A．

【解析】

（1）先根据三角形的内角和求出∠ABC+∠ACB=130°，再由角平分线定义得：∠PBC+∠PCB=65°，从而得出∠BPC的度数；

（2）与（1）同理可得：∠BPC=90°∠A；

（3）由外角平分线的定义得：∠PBC+∠PCB（∠DBC+∠BCE），并由两个平角和为360°和三角形内角和得出结论．

（1）∵∠A=50°，∴∠ABC+∠ACB=180°﹣50°=130°．

∵∠ABC与∠ACB的平分线交于点P，∴∠PBC∠ABC，∠PCB∠ACB，∴∠PBC+∠PCB∠ABC∠ACB（∠ABC+∠ACB）130°=65°，∴∠BPC=180°﹣65°=115°．

故答案为：115°；

（2）∵∠ABC+∠ACB=180°﹣∠A

由（1）得：∠PBC+∠PCB（∠ABC+∠ACB）（180°﹣∠A）=90°∠A，∴∠BPC=180°﹣（∠PBC+∠PCB）=180°﹣（90°∠A）=90°∠A．

故答案为：90°∠A．

（3）∵BP，CP分别是∠ABC与∠ACB的外角平分线，∴∠PBC∠DBC，∠PCB∠BCE，∴∠PBC+∠PCB（∠DBC+∠BCE）．

∵∠DBC+∠ABC+∠ACB+∠BCE=360°，∴∠DBC+∠BCE=360°﹣（∠ABC+∠ACB）=360°﹣（180°﹣∠A）=180°+∠A，∴∠PBC+∠PCB（180°+∠A）=90°∠A，∴∠BPC=180°﹣（∠PBC+∠PCB）=180°﹣（90°∠A）=90°∠A．

故答案为：90°∠A．