题目内容
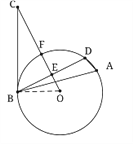
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点,且∠DBC=∠A,连接OE并延长与⊙O相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.

【答案】(1)证明见解析(2)9.6
【解析】试题分析:(1)连接OB,由垂径定理可得BE=DE,OE⊥BD,![]() ,再由圆周角定理可得
,再由圆周角定理可得![]() ,从而得到∠ OBE+∠ DBC=90°,即
,从而得到∠ OBE+∠ DBC=90°,即![]() ,命题得证.
,命题得证.
(2)由勾股定理求出OC,再由△OBC的面积求出BE,即可得出弦BD的长.
试题解析:(1)证明:如下图所示,连接OB.
∵ E是弦BD的中点,∴ BE=DE,OE⊥ BD,![]() ,
,
∴∠ BOE=∠ A,∠ OBE+∠ BOE=90°.
∵∠ DBC=∠ A,∴∠ BOE=∠ DBC,
∴∠ OBE+∠ DBC=90°,∴∠ OBC=90°,即BC⊥OB,∴ BC是⊙ O的切线.
(2)解:∵ OB=6,BC=8,BC⊥OB,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目



