Question

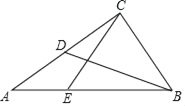
【题目】已知：如图，在Rt△ABC中，∠ACB=90°，BC=，cot∠ABC=，点D是AC的中点．

（1）求线段BD的长；

（2）点E在边AB上，且CE=CB，求△ACE的面积．

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）根据直角三角的特点，由∠ABC的正切值求出AC的长，然后根据中点的性质求出CD，再根据勾股定理可求解；

（2）过C作CH⊥AB于H，构造直角三角形，然后根据锐角三角函数求解.

试题解析：（1）Rt△ABC中，∠ACB=90°，BC=，cot∠ABC=，

∴AC= ，

∵点D是AC的中点，

∴CD=AC=，

∴Rt△BCD中，BD==；

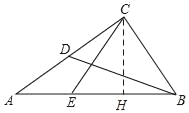
（2）如图，过C作CH⊥AB于H，

∵BC=，cot∠ABC=，

∴CH=，BH=2，

∵CE=CB，

∴EH=BH=1，

∵∠ACB=90°，BC=，AC=，

∴AB=3，

∴AE=3﹣2=1，

∴△ACE的面积=×AE×CH=×1×=．