题目内容
计算:
-9tan30°+(π-4)0-(
)-1.
| 12 |
| 1 |
| 2 |
考点:实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值
专题:
分析:分别根据数的开方法则、0指数幂及负整数指数幂的运算法则,特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可.
解答:解:原式=2
-9×
+1-2
=-
-1.
| 3 |
| ||
| 3 |
=-
| 3 |
点评:本题考查的是实数的运算,熟知数的开方法则、0指数幂及负整数指数幂的运算法则,特殊角的三角函数值是解答此题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,一小型水库堤坝的横断面为直角梯形,坝顶BC宽6m,坝高14m,斜坡CD的坡度i=1:2,则坝底AD的长为( )
如图,一小型水库堤坝的横断面为直角梯形,坝顶BC宽6m,坝高14m,斜坡CD的坡度i=1:2,则坝底AD的长为( )| A、13m | ||
| B、34m | ||
C、(6+14
| ||
| D、40m |
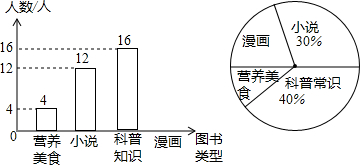
 为了解初三毕业生的体能情况,某校抽取了初三全年级500人中的一部分,初三毕业生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如右图),图中从左到右各小组的小长方形的面积之比是:2:4:1 7:1 5:9:3,第二小组的频数为12.试解答下列问题:
为了解初三毕业生的体能情况,某校抽取了初三全年级500人中的一部分,初三毕业生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如右图),图中从左到右各小组的小长方形的面积之比是:2:4:1 7:1 5:9:3,第二小组的频数为12.试解答下列问题: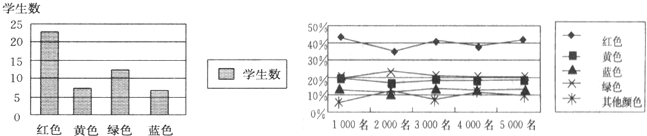
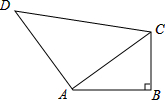 如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.
如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.