题目内容
10.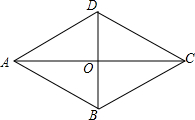 已知菱形ABCD的对角线AC=2$\sqrt{2}$+2,BD=2$\sqrt{2}$-2,求菱形的周长和面积.
已知菱形ABCD的对角线AC=2$\sqrt{2}$+2,BD=2$\sqrt{2}$-2,求菱形的周长和面积.
分析 先根据菱形的性质得AC⊥BD,OA=OC=$\frac{1}{2}$AC=$\sqrt{2}$+1,OB=OD=$\frac{1}{2}$BD=$\sqrt{2}$-1,再在Rt△AOB中利用勾股定理计算出AB=$\sqrt{6}$,然后根据菱形的周长定义和面积公式求解.
解答 解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=$\sqrt{2}$+1,OB=OD=$\frac{1}{2}$BD=$\sqrt{2}$-1,
在Rt△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(\sqrt{2}+1)^{2}+(\sqrt{2}-1)^{2}}$=$\sqrt{6}$,
∴菱形的周长=4AB=4$\sqrt{6}$;
菱形的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$•(2$\sqrt{2}$+2)(2$\sqrt{2}$-2)=2.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形的面积等于对角线乘积的一半.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
20.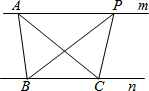 如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
 如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )| A. | AB∥PC | B. | △ABC的面积等于△BCP的面积 | ||
| C. | AC=BP | D. | △ABC的周长等于△BCP的周长 |
1.下列关系中,成反比例函数的是( )
| A. | 圆的面积S与半径r的关系 | |
| B. | 三角形的面积一定,它的底边a与这边上的高h的关系 | |
| C. | 人的年龄与身高的关系 | |
| D. | 小明从家到学校,剩下的路程s与速度v的关系 |
20.下列计算结果正确的是( )
| A. | 2a3+a3=3a6 | B. | (-a)2•a3=-a6 | C. | (a-b)2=a2-2ab+b2 | D. | (-2)0=-1 |

 如图,AB∥CD,∠1=120°,∠EDC的大小是60°.
如图,AB∥CD,∠1=120°,∠EDC的大小是60°.