题目内容
16.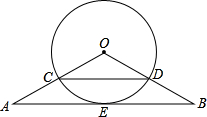 如图,△OAB中.OA=OB,∠A=30°,⊙O分别交OA、OB于C、D两点连接CD,E是AB的中点.
如图,△OAB中.OA=OB,∠A=30°,⊙O分别交OA、OB于C、D两点连接CD,E是AB的中点.(1)求证:CD∥AB.
(2)若AE=CD=4$\sqrt{3}$,求证:AB是⊙O的切线.
分析 (1)根据OC=OD,OA=OB,得到$\frac{OC}{OA}$=$\frac{OD}{OB}$,根据平行线的判定定理证明即可;
(2)连接OE,根据等腰三角形的三线合一得到OE⊥AB,根据题意和直角三角形的性质求出OE、OC的长,根据切线的判定定理证明即可.
解答 证明:(1)∵OC=OD,OA=OB,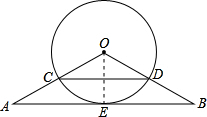
∴$\frac{OC}{OA}$=$\frac{OD}{OB}$,
∴CD∥AB;
(2)连接OE,
∵OA=OB,E是AB的中点,
∴OE⊥AB,又∠A=30°,
∴OE=4,
∵CD∥AB,
∴∠OCD=∠A=30°,
又∵CD=4$\sqrt{3}$,
∴OC=4,
∴OE=OC,
又OE⊥AB,
∴AB是⊙O的切线.
点评 本题考查的是切线的判定定理、平行线的判定定理、直角三角形的性质,切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
6.下列各题的两项是同类项的是( )
| A. | ab2与-$\frac{1}{2}$a2b | B. | xy2与x2y2 | C. | x3与y2 | D. | 3与-5 |
4.全国足球甲A联赛前12轮(场)比赛后,前三名比赛成绩如表:
问每队胜一场,平一场,负一场各得多少分?
| 胜(场) | 平(场) | 负(场) | 积分 | |
| 万达队 | 8 | 2 | 2 | 26 |
| 申花队 | 6 | 5 | 1 | 23 |
| 国安队 | 5 | 7 | 0 | 22 |