��Ŀ����
����Ŀ����ͼ��������y��![]() x2+bx+c��ֱ��y��
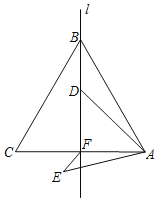
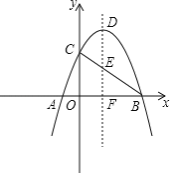
x2+bx+c��ֱ��y��![]() x+3�ֱ��ཻ��A��B���㣬�Ҵ���������x���һ������ΪC������AC��BC����֪A��0��3����C����3��0����
x+3�ֱ��ཻ��A��B���㣬�Ҵ���������x���һ������ΪC������AC��BC����֪A��0��3����C����3��0����
��1���������ߵĽ���ʽ��
��2���������߶Գ���l����һ��M��ʹ|MB��MC|��ֵ������������ֵ��
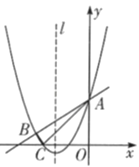
��3����PΪy���Ҳ���������һ���㣬����PA������P��PQ��PA��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ��������������ABC���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��![]() x2+
x2+![]() x+3����2��|MB��MC|ȡ���ֵΪ
x+3����2��|MB��MC|ȡ���ֵΪ![]() ����3�����ڣ���P��1��6����
����3�����ڣ���P��1��6����
��������
��1���ٽ�A��0��3����C��-3��0������y=![]() x2+bx+c��������⣻
x2+bx+c��������⣻
��2���ֵ���B��C��M���㲻����ʱ������B��C��M���㹲��ʱ����������ֱ���⼴�ɣ�
��3���ֵ�![]() ʱ����
ʱ����![]() ʱ����������ֱ���⼴�ɣ�
ʱ����������ֱ���⼴�ɣ�
��1����A��0��3����C����3��0������y��![]() x2+bx+c��
x2+bx+c��
�� ��
��
���![]() ��
��
�������ߵĽ���ʽ��y��![]() x2+
x2+![]() x+3��
x+3��
��2����ֱ��y��![]() x+3����ʽ����κ�������ʽ��������ã�x��0��4��
x+3����ʽ����κ�������ʽ��������ã�x��0��4��
��A ��0��3����
��B����4��1��
�ٵ���B��C��M���㲻����ʱ��
|MB��MC|��BC��
�ڵ���B��C��M���㹲��ʱ��
|MB��MC|��BC��
�൱�㡢C��M���㹲��ʱ��|MB��MC|ȡ���ֵ����ΪBC�ij���
����B��x���ڵ�E��

��Rt��BEC�У��ɹ��ɶ�����BC��![]() ��
��![]() ��
��
��|MB��MC|ȡ���ֵΪ![]() ��
��
��3�����ڵ�Pʹ����A��P��QΪ���������������ABC���ƣ�
���P������x��![]() x2+
x2+![]() x+3����x��0��
x+3����x��0��
��Rt��BEC��
��BE��CE��1��
���BCE��45����
��Rt��ACO��
��AO��CO��3��
���ACO��45����
���ACB��180����450��450��900��AC��3![]() ��
��
����P��PQ��PA�ڵ�P�����APQ��90��������P��PQ��y���ڵ�G��

�ߡ�PQA����APQ��90��
��PAG����QAP��
���PGA�ס�QPA
�ߡ�PGA����ACB��90��
��ٵ�![]() ʱ��
ʱ��
��PAG�ס�BAC��
�� ��
��
���x1��1��x2��0������ȥ��
���P��������Ϊ![]() ��12+
��12+![]() ��1+3��6��
��1+3��6��
���P��1��6����
�ڵ�![]() ʱ��
ʱ��
��PAG�ס�ABC��
�� ��
��
���x1����![]() ����ȥ����x2��0����ȥ����
����ȥ����x2��0����ȥ����
���ʱ���������ĵ�P
�������������ڵ�P��1��6����