题目内容
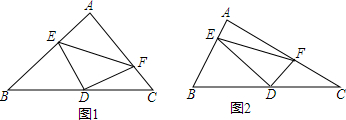
12.如图,△ABC是直角三角形,∠CAB=90°,D是斜边BC上的中点,一块直角三角板直角顶点与D重合,绕D转动,直角三角板的两直角边分别与AB,AC交于E、F.(1)(如图1)若AB=AC,直角三角形在转动过程中是否始终有DE=DF,并说明理由.
(2)(如图1)若AB=AC,BE=12,CF=5,求△DEF的面积.
(3)(如图1)若AB=AC,求证:BE2+CF2=EF2.
(4)(如图2)若AB≠AC,是否仍然有BE2+CF2=EF2成立?并说明理由.
分析 (1)连接AD,由等腰直角三角形的性质得出∠DAC=∠BAD=∠C=45°,AD⊥BC,AD=BD=DC,证出∠EDA=∠CDF,由ASA证明△AED≌△CFD,得出AE=CF,DE=DF即可;(2)证出BE=AF,根据勾股定理求出EF,解直角三角形求出DE和DF,根据三角形面积公式即可得出结果.
(3)由(1)得:AE=CF,BE=AF,由勾股定理即可得出结论.
(4)延长ED至G,使GD=ED,连接CG,则DF垂直平分EG,由线段垂直平分线的性质得出EF=GF,由SAS证明△BDE≌△CDG,得出BE=CG,∠B=∠DCG,证出∠FCG=90°,由勾股定理即可得出结果.
解答 (1)解:始终有DE=DF,理由如下:
连接AD,如图1所示: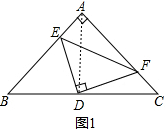
∵在Rt△ABC中,AB=AC,AD为BC边的中线,
∴∠DAC=∠BAD=∠C=45°,AD⊥BC,AD=$\frac{1}{2}$BC=BD=DC,
又∵DE⊥DF,AD⊥DC,
∴∠EDA+∠ADF=∠CDF+∠FDA=90°,
∴∠EDA=∠CDF,
在△AED与△CFD中,$\left\{\begin{array}{l}{∠EDA=∠CDF}&{\;}\\{AD=CD}&{\;}\\{∠EAD=∠C}&{\;}\end{array}\right.$,
∴△AED≌△CFD(ASA).
∴AE=CF,DE=DF;
(2)解:∵AB=AC,AE=CF,
∴BE=AF=12,
∴EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=13,
∵DE=DF,∠EDF=90°,
∴在Rt△EDF中,由勾股定理得:ED2+DF2=EF2=132,
DE=DF=$\frac{13\sqrt{2}}{2}$,
∴△DEF的面积S=$\frac{1}{2}$×DE×DF=$\frac{1}{2}$×$\frac{13\sqrt{2}}{2}$×$\frac{13\sqrt{2}}{2}$=$\frac{169}{4}$;
(3)证明:∵AB=AC,∠CAB=90°,
由(1)得:AE=CF,BE=AF,
∴BE2+CF2=AF2+AE2=EF2.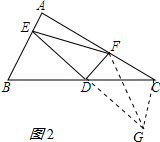
(4)解:BE2+CF2=EF2成立;理由如下:
延长ED至G,使GD=ED,连接CG、FG,如图2所示:
则DF垂直平分EG,
∴EF=GF,
在△BDE和△CDG中,$\left\{\begin{array}{l}{BD=CD}&{\;}\\{∠BDE=∠CDG}&{\;}\\{ED=GD}&{\;}\end{array}\right.$,
∴△BDE≌△CDG(SAS),
∴BE=CG,∠B=∠DCG,
∵∠B+∠ACB=90°,
∴∠DCG+∠ACB=90°,
即∠FCG=90°,
∴CG2+CF2=GF2,
∴BE2+CF2=EF2.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质、线段垂直平分线的性质、勾股定理、三角形面积的计算方法;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

 如图是由一些相同的小正方体构成的几何体从不同方向看得到的平面图形,这些相同的小正方体的个数是5.
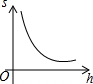
如图是由一些相同的小正方体构成的几何体从不同方向看得到的平面图形,这些相同的小正方体的个数是5. 如图,已知点P是y轴正半轴上任意一点,过点P作x轴的平行线交抛物线y=x2于点C,D(点C在点D的右边),过点C作CB⊥x轴于点B,过点D作DA⊥x轴于点A,分别以OA,OB为直径作半圆.设点P的纵坐标为h,图中阴影部分的面积为s,则s与h之间的函数关系的图象大致是( )
如图,已知点P是y轴正半轴上任意一点,过点P作x轴的平行线交抛物线y=x2于点C,D(点C在点D的右边),过点C作CB⊥x轴于点B,过点D作DA⊥x轴于点A,分别以OA,OB为直径作半圆.设点P的纵坐标为h,图中阴影部分的面积为s,则s与h之间的函数关系的图象大致是( )