题目内容
1.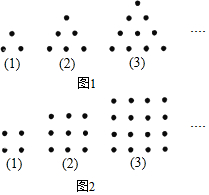 古希腊人常用小石子在沙滩上摆成各种形状来研究数,在图1中,依次摆成第(1),(2),(3),(4)…个三角形状的小石子数3,6,10,…称为三角形数;在图2中,依次摆成第(1),(2),(3),(4),…个正方形状的小石子数4,9,16,…称为正方形数.
古希腊人常用小石子在沙滩上摆成各种形状来研究数,在图1中,依次摆成第(1),(2),(3),(4)…个三角形状的小石子数3,6,10,…称为三角形数;在图2中,依次摆成第(1),(2),(3),(4),…个正方形状的小石子数4,9,16,…称为正方形数.(1)请写出第(4)个三角形数15,第(4)个正方形数25;
(2)请写出第(n)个三角形数$\frac{(n+1)(n+2)}{2}$,第(n)个正方形数(n+1)2;
(3)请写出2个既是三角形数又是正方形数的数36、1225.
分析 (1)由第n个三角形数为1+2+3+…+n+1即可得,第n个正方形数为(n+1)2;
(2)由(1)可得;
(3)既是三角形数又是正方形数的数36、1225.
解答 解:(1)由题意知第(4)个三角形数为1+2+3+4+5=15,第(4)个正方形数52=25,
故答案为:15、25;
(2)第(n)个三角形数为1+2+3+…+n+1=$\frac{(n+1)(n+2)}{2}$,
第(n)个正方形数(n+1)2,
故答案为:$\frac{(n+1)(n+2)}{2}$,(n+1)2;
(3)既是三角形数又是正方形数的数36、1225,
故答案为:36、1225.
点评 此题考查了图形的变化类,解题时让学生通过观察、分析和归纳得出其中的规律是解题的关键.

练习册系列答案
相关题目
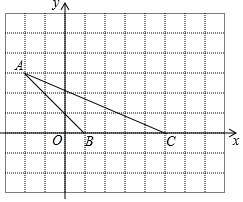 如图所示,小方格边长为1个单位,
如图所示,小方格边长为1个单位,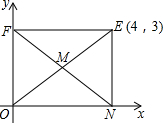 【阅读】
【阅读】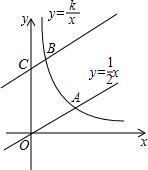 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移4个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,OA=3BC.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移4个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,OA=3BC.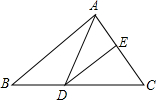 如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm.
如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm.