��Ŀ����
4���Ķ����ϣ��ڰ�˫�ۣ��ݺὭ����˫����赣������У���������С˵�еij�������������ָ�����˺���һ��ȡ�����̣������ޱȣ��ڶ��θ�ʽ��Ҳ�������ศ��ɵ����ӣ��磨2+$\sqrt{3}$����2-$\sqrt{3}$��=22-��-$\sqrt{3}$��2=1����$\sqrt{5}$+$\sqrt{2}$����$\sqrt{5}$-$\sqrt{2}$��=��$\sqrt{5}$��2-��$\sqrt{2}$��2=3�����ǵĻ���������������˵���������θ�ʽ��Ϊ��������ʽ������һ������һ�������������أ����ǣ����ǿ��Խ������ʽ�ӻ���
$\frac{1}{2-\sqrt{3}}$=$\frac{2+\sqrt{3}}{��2-\sqrt{3}����2+\sqrt{3}��}$=2+$\sqrt{3}$
������⣺
��1��4+$\sqrt{7}$��һ����������ʽ��4-$\sqrt{7}$��
��2�����㣺$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+��+$\frac{1}{\sqrt{2017}+\sqrt{2015}}$��
���� ��1��д��ԭʽ��һ����������ʽ���ɣ�
��2��ԭʽ�����ĸ���������㼴�ɵõ������
��� �⣺��1��4+$\sqrt{7}$��һ����������ʽ��4-$\sqrt{7}$��
�ʴ�Ϊ��4-$\sqrt{7}$��
��2��ԭʽ=$\frac{1}{2}$��$\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$+��+$\sqrt{2017}$-$\sqrt{2015}$��=$\frac{\sqrt{2017}-1}{2}$��
���� ���⿼���˷�ĸ����������ȷѡ���������θ�ʽ��ʹ���ǵĻ�����ƽ���ʽ�ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
15����ͼ����ӳ���������У�����y��x�ĺ����ĸ����У�������


| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
13������$\frac{{x}^{2}}{x-1}$-x+1�Ľ���ǣ�������
| A�� | $\frac{1}{x-1}$ | B�� | $\frac{1}{1-x}$ | C�� | $\frac{1-2x}{x-1}$ | D�� | $\frac{2x-1}{x-1}$ |
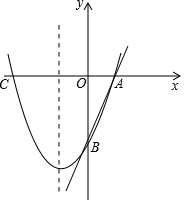 ��ͼ����ֱ֪��y=3x-3�ֱ�x�ᡢy����A��B���㣬������y=x2+bx+c����
��ͼ����ֱ֪��y=3x-3�ֱ�x�ᡢy����A��B���㣬������y=x2+bx+c����