题目内容
15.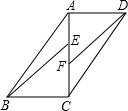 如图,平行四边形ABCD中,AC⊥AD,BE∥DF,若AD=5cm,CF=3cm,EF=2cm,则DF=5$\sqrt{2}$cm.
如图,平行四边形ABCD中,AC⊥AD,BE∥DF,若AD=5cm,CF=3cm,EF=2cm,则DF=5$\sqrt{2}$cm.
分析 根据平行四边形的性质,由AAS证△BEC≌△DFA,得出BE=DF,再由SAS证△AEB≌△CFD,得到AE=CF,然后根据勾股定理即可求出结果.
解答 解:?ABCD中,BE∥DF,
∴BC=AD,∠DFA=∠BEC,∠AEB=∠CFD,
又∵AC⊥AD,
∴∠ACB=∠CAD=90°,
在△BEC和△DFA中,
$\left\{\begin{array}{l}{BC=AD}\\{∠DFA=∠BEC}\\{∠ACB=∠CAD}\end{array}\right.$,
∴△BEC≌△DFA(AAS),
∴BE=DF,
∵BE∥DF,
∴∠BEC=∠AFD,
∵四边形ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
∴∠ABE=∠CDF,
在△AEB和△CFD中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠CDF}\\{BE=DF}\end{array}\right.$,
∴△AEB≌△CFD(SAS),
∴AE=CF=3cm,
又∵在Rt△FAD中,AF=AE+EF=3+2=5cm,AD=5cm,
∴根据勾股定理得DF=$\sqrt{A{F}^{2}+A{D}^{2}}$=$\sqrt{{5}^{2}+{5}^{2}}$5$\sqrt{2}$=5(cm).
故答案为:5$\sqrt{2}$.
点评 本题考查平行四边形的性质、平行线的性质、全等三角形的判定与性质、勾股定理等知识,熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
10.给出五种图形:①矩形,②菱形,③等腰三角形(腰与底边不相等),④等边三角形,⑤平行四边形(不含矩形,菱形).其中可用两块能完全重合的含有30°角的三角板拼成的所有图形是( )
| A. | ①、②、③ | B. | ②、④、⑤ | C. | ①、③、④、⑤ | D. | ①、②、③、④、⑤ |
4.已知sinA=$\frac{1}{2}$,∠A为锐角,则cos2A等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 五边形ABCDE的各内角度数如图所示,则x=75.
五边形ABCDE的各内角度数如图所示,则x=75.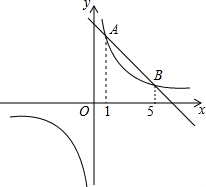 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,它们的横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}-b$的解集是0<x<1或x>5.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,它们的横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}-b$的解集是0<x<1或x>5.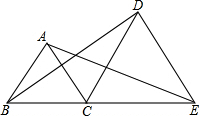 如图,已知B、C、E在同一条直线上,△ABC和△DCE均为等边三角形,连结AE、BD.
如图,已知B、C、E在同一条直线上,△ABC和△DCE均为等边三角形,连结AE、BD.