题目内容
5.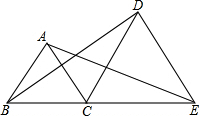 如图,已知B、C、E在同一条直线上,△ABC和△DCE均为等边三角形,连结AE、BD.
如图,已知B、C、E在同一条直线上,△ABC和△DCE均为等边三角形,连结AE、BD.(1)求证:AE=BD.
(2)若把△DEF绕点C顺时针再旋转一个角度,(1)中的结论还成立吗?请画出图形进行说明.
分析 (1)根据等边三角形边长相等的性质和各内角为60°的性质可求得△BCD≌△ACE,根据全等三角形对应边相等的性质即可求得AE=BD.
(2)根据题意画出图形,证明方法与(1)相同.
解答 解:(1)∵△ABC、△DCE均为等边三角形,
∴BC=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCA+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
∵在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴AE=BD;
(2)成立;
如图:∵△ABC、△DCE均为等边三角形,
∴BC=AC,CD=CE,∠BCA=∠DCE=60°,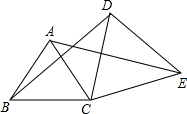
∴∠BCA+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
∵在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴AE=BD.
点评 本题考查了等边三角形的判定与性质、全等三角形的判定与性质.等边三角形的三条边都相等,三个内角都是60°,解决本题的根据是证明△ACE≌△BCD.

练习册系列答案
相关题目
10.下列图形是中心对称图形但不是轴对称图形的是( )
| A. | 正三角形 | B. | 平行四边形 | C. | 菱形 | D. | 圆 |
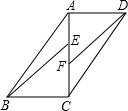 如图,平行四边形ABCD中,AC⊥AD,BE∥DF,若AD=5cm,CF=3cm,EF=2cm,则DF=5$\sqrt{2}$cm.
如图,平行四边形ABCD中,AC⊥AD,BE∥DF,若AD=5cm,CF=3cm,EF=2cm,则DF=5$\sqrt{2}$cm. 如图,Rt△DAC与Rt△EBC,CD⊥CE,求证:∠D=∠ECB.
如图,Rt△DAC与Rt△EBC,CD⊥CE,求证:∠D=∠ECB.