题目内容
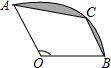 如图,扇形OAB的半径OA=2,圆心角∠AOB=120°,点C是弧
如图,扇形OAB的半径OA=2,圆心角∠AOB=120°,点C是弧 |
| AB |
 |
| AC |
 |
| CB |
考点:扇形面积的计算
专题:
分析:要使阴影部分的面积最小,就需要满足四边形AOBC的面积最大,连接AB,只需满足△ABC的面积最大即可,从而确定点C的位置,点C位于弧AB的中点,从而求出四边形AOBC的面积,由2(S扇形AOC-S△AOC),即可得出答案.
解答: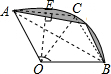 解:连接AB,CO,过点O作OE⊥AC于点E,
解:连接AB,CO,过点O作OE⊥AC于点E,
要使阴影部分的面积最小,就需要满足四边形AOBC的面积最大,只需满足△ABC的面积最大即可,
从而可得当点C位于弧AB的中点时,△ABC的面积最大,
则OC⊥AB,
∵∠AOB=120°,
∴∠AOC=∠BOC=60°,
∵OA=CO=BO=2,
∴△AOC和△BOC是等边三角形,
∴AC=BC=2,
∴EC=1,则EO=
,
故S△AOC=
×AC×EO=
×2×
=
,
故弓形AC的面积为:S扇形AOC-S△AOC=
-
=
-
,
可得S阴影=2(S扇形AOC-S△AOC)=
-2
.
故答案为:
-2
.
 解:连接AB,CO,过点O作OE⊥AC于点E,
解:连接AB,CO,过点O作OE⊥AC于点E,要使阴影部分的面积最小,就需要满足四边形AOBC的面积最大,只需满足△ABC的面积最大即可,
从而可得当点C位于弧AB的中点时,△ABC的面积最大,
则OC⊥AB,
∵∠AOB=120°,
∴∠AOC=∠BOC=60°,
∵OA=CO=BO=2,
∴△AOC和△BOC是等边三角形,
∴AC=BC=2,
∴EC=1,则EO=
| 3 |
故S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故弓形AC的面积为:S扇形AOC-S△AOC=
| 60π×22 |
| 360 |
| 3 |
| 2π |
| 3 |
| 3 |
可得S阴影=2(S扇形AOC-S△AOC)=
| 4π |
| 3 |
| 3 |
故答案为:
| 4π |
| 3 |
| 3 |
点评:本题考查了扇形的面积计算及动点问题,解答本题的关键是判断出点C的位置,有一定难度.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,CD为△ABC的角平分线,∠DCB=30°,BC=AC+AD,求∠A的度数.
如图,CD为△ABC的角平分线,∠DCB=30°,BC=AC+AD,求∠A的度数.

 如图,已知点B在x轴的负半轴上,AB⊥x轴于点B,AB=1,∠AOB=30°,求点A的坐标.
如图,已知点B在x轴的负半轴上,AB⊥x轴于点B,AB=1,∠AOB=30°,求点A的坐标. 如图,在?ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4
如图,在?ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4