题目内容
在一个等腰钝角三角形中，一个内角的度数是另一个内角度数的3倍，那么顶角是 度，底角是 度．
考点：等腰三角形的性质
专题：
分析：根据三角形的内角和是180°，以及等腰钝角三角形的性质特点从而求得三角形的每个角的度数．
解答：解：设这个三角形的底角的度数为x，则顶角的度数为3x，
则有2x+3x=180°，
解得x=36°，
3x=108°，
所以这个三角形的顶角是108°，底角是36°，
故答案为：108、36．
则有2x+3x=180°，
解得x=36°，
3x=108°，
所以这个三角形的顶角是108°，底角是36°，
故答案为：108、36．
点评：本题考查了三角形的内角和定理以及等腰钝角三角形的性质特点．
练习册系列答案
阅读快车系列答案
相关题目
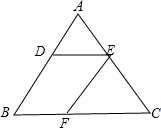如图，在△ABC中，DE∥BC，交AB于点D，交AC于点E，EF∥AB交BC于点F，已知△ADE的面积为4，△EFC的面积为9，则△ABC的面积为
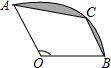如图，扇形OAB的半径OA=2，圆心角∠AOB=120°，点C是弧