题目内容
在四边形ABCD中,AB,BC,CD,DA的中点分别为P,Q,M,N;
(1)如图1,试判断四边形PQMN为怎样的四边形,并证明你的结论.
(2)若在AB上取一点E,连结DE,CE,恰好△ADE和△BCE都是等边三角形.
①判断此时四边形PQMN的形状,并证明你的结论;
②当AE=6,EB=3,求此时四边形PQMN的周长.
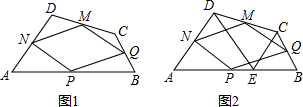
(1)如图1,试判断四边形PQMN为怎样的四边形,并证明你的结论.
(2)若在AB上取一点E,连结DE,CE,恰好△ADE和△BCE都是等边三角形.
①判断此时四边形PQMN的形状,并证明你的结论;
②当AE=6,EB=3,求此时四边形PQMN的周长.

考点:中点四边形
专题:
分析:(1)连结AC、BD.利用三角形中位线定理判定四边形PQMN的对边平行且相等,易证该四边形是平行四边形;
(2)①设△ADE的边长是x,△BCE的边长是y,由于DB2=(
x+y)2+(
x)2=x2+xy+y2,AC=(x+
y)2+(
y)2=x2+xy+y2,可得平行四边形PQMN的对角线相等,从而得出平行四边形PQMN是菱形;
②如图2,过点D作DF⊥AB于F,则通过解三角形求得DF=3
,由勾股定理得到DB.由①知四边形PQMN是菱形,可计算得周长是6
.
(2)①设△ADE的边长是x,△BCE的边长是y,由于DB2=(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
②如图2,过点D作DF⊥AB于F,则通过解三角形求得DF=3
| 3 |
| 7 |
解答:解:(1)连结AC、BD.
∵PQ为△ABC的中位线,
∴PQ∥AC,PQ=
AC,
同理MN∥AC.MN=
AC.
∴MN=PQ,MN∥PQ,
∴四边形PQMN为平行四边形;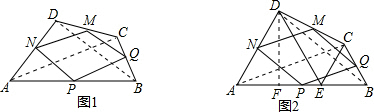
(2)①四边形PQMN是菱形;
理由如下:设△ADE的边长是x,△BCE的边长是y,
∴DB2=(
x+y)2+(
x)2=x2+xy+y2,AC2=(x+
y)2+(
y)2=x2+xy+y2,
∵平行四边形PQMN的对角线相等,
∴平行四边形PQMN是菱形;
②过点D作DF⊥AB于F,则DF=3
又∵DF2+FB2=DB2
∴DB=3
∴由①知四边形PQMN是菱形,可计算得周长是6
.
∵PQ为△ABC的中位线,
∴PQ∥AC,PQ=
| 1 |
| 2 |
同理MN∥AC.MN=
| 1 |
| 2 |
∴MN=PQ,MN∥PQ,
∴四边形PQMN为平行四边形;
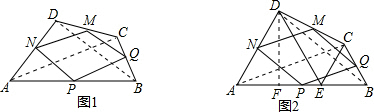
(2)①四边形PQMN是菱形;
理由如下:设△ADE的边长是x,△BCE的边长是y,
∴DB2=(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∵平行四边形PQMN的对角线相等,
∴平行四边形PQMN是菱形;
②过点D作DF⊥AB于F,则DF=3
| 3 |
又∵DF2+FB2=DB2
∴DB=3
| 7 |
∴由①知四边形PQMN是菱形,可计算得周长是6
| 7 |
点评:本题考查了中点四边形以及菱形的判定和性质、平行四边形的判定和性质,解题时,利用了三角形中位线的性质定理.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
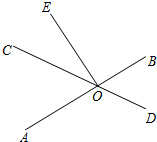 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=30°,求∠AOD的度数.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=30°,求∠AOD的度数.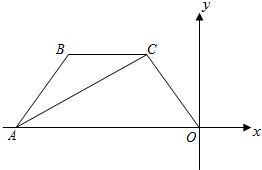 如图,在平面直角坐标系中,四边形OABC的顶点A在x轴上,OA∥BC,∠BAC=∠BCA,OA=4,BC=2,点C的坐标为(-1,
如图,在平面直角坐标系中,四边形OABC的顶点A在x轴上,OA∥BC,∠BAC=∠BCA,OA=4,BC=2,点C的坐标为(-1, 如图,四边形ABCD,在四边形内找一点O,使得线段AO、BO、CO、DO的和最小.(画出即可,不写作法)
如图,四边形ABCD,在四边形内找一点O,使得线段AO、BO、CO、DO的和最小.(画出即可,不写作法)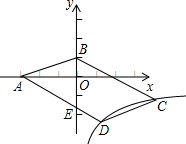 如图,?ABCD的顶点A,B的坐标分别是A(-3,0)、B(0,1),顶点C、D在双曲线y=
如图,?ABCD的顶点A,B的坐标分别是A(-3,0)、B(0,1),顶点C、D在双曲线y=