题目内容
14.同圆中,内接正六边形与内接正方形的面积比是3$\sqrt{3}$:4.分析 将圆内接正四边形和圆内接正六边形的边长用圆的半径表示出来,再求出圆内接正四边形与正六边形的面积表达式(用圆的半径表示),然后即可得出其面积比.
解答 解:设圆的半径为r.如图: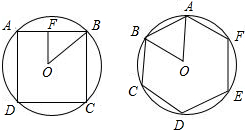
在正方形ABCD中,作边心距OF,
则OF=OBsin45°=$\frac{\sqrt{2}}{2}$r,
则AD=2×$\frac{\sqrt{2}}{2}$r=$\sqrt{2}$r,
圆内接正四边形的面积为SABCD=($\sqrt{2}$r)2=2r2;
在正六边形ABCDEF中,
AB=BO=OA=r,
则SABCDEF=6×$\frac{1}{2}$OA•OBsin60°,
=6×$\frac{1}{2}$r•rsin60°,
=6×$\frac{\sqrt{3}}{4}$r2,
=$\frac{3\sqrt{3}}{2}$r2,
SABCDEF:SABCD=$\frac{3\sqrt{3}}{2}$r2:2r2=3$\sqrt{3}$:4;
故答案为:3$\sqrt{3}$:4.
点评 此题主要考查正多边形的计算问题,属于常规题.解答时要熟悉正方形和正六边形的面积计算方法,尤其要懂得分割计算再求和.

练习册系列答案
相关题目
5.一组数据如下:3,6,7,2,3,4,3,6,那么这组数据的中位数和众数分别是( )
| A. | 3,3 | B. | 3.5,3 | C. | 4,3 | D. | 3.5,6 |