题目内容
8.计算:(1)$\frac{1}{1×2}$+$\frac{1}{2×3}+\frac{1}{3×4}$+…+$\frac{1}{19×20}$;
(2)$\frac{1}{1×4}+\frac{1}{4×7}+\frac{1}{7×10}$+…+$\frac{1}{91×94}$.
分析 (1)拆成以这两个因数为分母,分子是1的差,再进一步计算即可;
(2)提取$\frac{1}{3}$,拆成以这两个因数为分母,分子是1的差,再进一步计算即可.
解答 解:(1)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{19}$-$\frac{1}{20}$
=1-$\frac{1}{20}$
=$\frac{19}{20}$;
(2)原式=$\frac{1}{3}$×(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{10}$+…+$\frac{1}{91}$-$\frac{1}{94}$)
=$\frac{1}{3}$×(1-$\frac{1}{94}$)
=$\frac{31}{94}$.
点评 此题考查有理数的混合运算,掌握拆分的方法是解决问题的关键.

练习册系列答案
相关题目
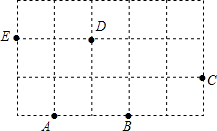 如图,过A、B、C、D、E五个点中的任意三点画三角形.
如图,过A、B、C、D、E五个点中的任意三点画三角形.