题目内容
12.平面内的两条直线有相交和平行两种位置关系(1)已知AB平行于CD,如a图,当点P在AB、CD外部时,∠BPD+∠D=∠B即∠BPD=∠B-∠D,为什么?请说明理由.如b图,将点P移动到AB、CD内部,以上结论是否仍然成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.

分析 (1)①利用平行线的性质和三角形的外角即可;②利用平行线的特点作出平行线,再利用平行线的性质即可;
(2)利用三角形的外角等于与它不相邻的两内角的和即可;
(3)利用三角形的外角的性质把角转化到四边形CDHM中,用四边形的内角和即可.
解答 解:(1)①∵AB∥CD,
∴∠B=∠COP,
∵∠COP=∠BPD+∠D,
∴∠B=∠BPD+∠D,
即:∠BPD=∠B-∠D,
②不成立,
结论:∠BPD=∠B+∠D,
理由:如图b,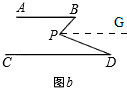
过点P作PG∥AB,
∴∠B=∠BPG,
∵PG∥AB,CD∥AB,
∴PG∥CD,
∴∠DPG=∠D,
∴∠BPD=∠BPG+∠DPG=∠B+∠D;
(2)结论:∠DPQ=∠B+∠BQD+∠D,
理由:如图c,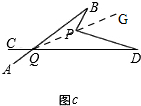
连接QP并延长,
∵∠BP∠G是△BPQ的外角,
∴∠BPG=∠B+∠BQP,
同理:∠DPG=∠D+∠DQP,
∴∠BPD=∠BPG+∠DPG=∠B+∠BQP+∠DQP+∠D=∠B+∠BQD+∠D;
(3)如图d,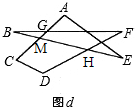
∵∠DHM是△BFH的外角,
∴∠DHM=∠B+∠F,
同理:∠CMH=∠A+∠E,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠DHM+∠CMH+∠C+∠D=360°.
点评 此题是四边形的性质,主要考查了平行线的性质和判定,三角形的外角的性质,四边形的内角和,解本题的关键是作出辅助线,是一个比较简单也比较典型的中考常考题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
3.若函数y=x2+(a-2)|x|-2a的图象与x轴有且仅有两个不同的交点,则实数a的取值范围是( )
| A. | a=-2 | B. | a>0 | C. | a=-2或a>0 | D. | a≤-2或a>0 |
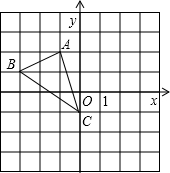 如图,若将△ABC绕点C逆时针旋转90°后得到△A′B′C′,
如图,若将△ABC绕点C逆时针旋转90°后得到△A′B′C′, 图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB和CD的端点A、B、C、D均在格点上.
图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB和CD的端点A、B、C、D均在格点上. 下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )



 已知如图,AD∥CF∥EB,AB=3,AC=5,DF=9,DA=2,CF=8,则,DE=$\frac{27}{5}$,EF=$\frac{18}{5}$,BE=4.
已知如图,AD∥CF∥EB,AB=3,AC=5,DF=9,DA=2,CF=8,则,DE=$\frac{27}{5}$,EF=$\frac{18}{5}$,BE=4.