题目内容
11．
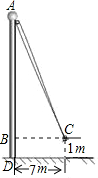如图1，小红将升旗的绳子拉到旗杆顶端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆7m处，发现此时绳子末端距离地面1m，则绳子的长度为（ ）| A． | 25m | B． | 4m | C． | 16m | D． | 17m |
分析 根据题意画出示意图，设旗杆高度为x，可得AC=AD=x，AB=（x-1）m，BC=7m，在Rt△ABC中利用勾股定理可求出x．
解答 解：设旗杆高度为x，则AC=AD=x，AB=（x-1）m，BC=7m，
在Rt△ABC中，AB2+BC2=AC2，即（x-1）2+72=x2，
解得：x=25，
即旗杆的高度为25米．
故选：A．
点评 本题考查了勾股定理的应用，解答本题的关键是构造直角三角形，构造直角三角形的一般方法就是作垂线．
练习册系列答案
相关题目
1．
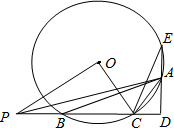如图，△ABC内接于⊙O，AD⊥BC于D交⊙O于E
（1）若∠ACB=120°，求证：CE=⊙O的半径．
（2）连OC，OP⊥OC交CB的延长线于P，若⊙O的半径为5cm，弦BC=6cm，求PB的长．
如图，△ABC内接于⊙O，AD⊥BC于D交⊙O于E（1）若∠ACB=120°，求证：CE=⊙O的半径．
（2）连OC，OP⊥OC交CB的延长线于P，若⊙O的半径为5cm，弦BC=6cm，求PB的长．
2．
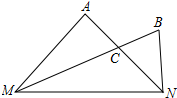如图，在MN的同侧作△AMN和△BMN，BM平分∠AMN，AN平分∠BNM，AN交BM于点C．设∠A=α°，∠B=β°，下列结论不正确的是（ ）
如图，在MN的同侧作△AMN和△BMN，BM平分∠AMN，AN平分∠BNM，AN交BM于点C．设∠A=α°，∠B=β°，下列结论不正确的是（ ）| A． | 若α=β，则点C在MN的垂直平分线上 | |
| B． | 若α+β=180°，则∠AMB=∠NMB | |
| C． | ∠MCN=$（\frac{α+β}{3}+60）$° | |
| D． | 当∠MCN=120°时，延长MA、NB交于点O，则OA=OB |
浠水县某中学规划在校园内一块长36米，宽20米的矩形场地ABCD上修建三条同样宽的人行道，使其中两条与AB平行，另一条与AD平行，其余部分种草，（如图所示），若使每一块草坪的面积都为96平方米，则人行道的宽为多少米？
6．如果x2-kxy+4y2是关于x、y的完全平方式，那么k的值是（ ）
| A． | 2 | B． | 4 | C． | -4 | D． | 4或-4 |
16．
如图，设数轴上的点A，B，C表示的数分别为a，b，c，则下列说法中错误的是（ ）
如图，设数轴上的点A，B，C表示的数分别为a，b，c，则下列说法中错误的是（ ）| A． | a＜0 | B． | b＞0 | C． | c＞b | D． | a-b＞0 |
20．计算（-$\frac{1}{2}$x3y）2的结果是（ ）
| A． | $\frac{1}{2}$x4y2 | B． | -$\frac{1}{4}$x6y2 | C． | $\frac{1}{4}$x6y2 | D． | $\frac{1}{2}$x6y2 |