题目内容
 矩形ABCD中,AB=3,BC=5. E为CD边上一点,将矩形沿直线BE折叠,使点C落在AD边上C′处.求DE的长.
矩形ABCD中,AB=3,BC=5. E为CD边上一点,将矩形沿直线BE折叠,使点C落在AD边上C′处.求DE的长.考点:翻折变换(折叠问题)
专题:
分析:由BE为折痕,可得B′C=BC,C′E=CE,在直角三角形ABC′中,求出AC′的大小,得到C′D,设出DE=x,表示出C′E的长度,在Rt△C′DE通过勾股定理可求得答案.
解答:解:设DE=xcm,则EC=(CD-x)cm,
∵矩形ABCD中,AB=3,BC=5,
∴BC=AD=5,CD=AB=3,
∵BE为折痕,
∴BC′=BC=5,C′E=CE=3-x,
Rt△ABC′中,AC′=
=
=4,
∴C′D=5-4=1,
Rt△C′DE中,C′E2=C′D2+DE2,
即(3-x)2=12+x2,
解得x=
.
即DE=
.
∵矩形ABCD中,AB=3,BC=5,
∴BC=AD=5,CD=AB=3,
∵BE为折痕,
∴BC′=BC=5,C′E=CE=3-x,
Rt△ABC′中,AC′=
| BC′2-AB2 |
| 52-32 |
∴C′D=5-4=1,
Rt△C′DE中,C′E2=C′D2+DE2,
即(3-x)2=12+x2,
解得x=
| 4 |
| 3 |
即DE=
| 4 |
| 3 |
点评:本题考查了翻折变换问题;由翻折得到相等的线段,两次利用勾股定理是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,点A(-2,-3)关于x轴对称点A′的坐标是( )
| A、(2,3) |
| B、(3,-2) |
| C、(-2,3) |
| D、(-3,-2) |
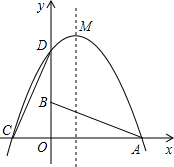 如图,已知△OAB的顶点A(3,0),B(0,1),O是坐标原点.将△OAB绕点O按逆时针旋转90°得到△ODC.
如图,已知△OAB的顶点A(3,0),B(0,1),O是坐标原点.将△OAB绕点O按逆时针旋转90°得到△ODC.
 已知实数a、b、c在数轴上的位置如图,化简:
已知实数a、b、c在数轴上的位置如图,化简: