题目内容
3.因式分解:(1)2a3-8a
(2)4a(x-y)-2b(y-x);
(3)(x2+4)2-16x2
(4)(x-y)2+4xy.
分析 (1)先提取公因式2a,再对余下的多项式利用平方差公式继续分解;
(2)提取公因式2(x-y),整理即可得解;
(3)先利用平方差公式分解因式,再利用完全平方公式继续分解;
(4)先利用完全平方公式展开,整理后利用完全平方公式继续分解.
解答 解:(1)2a3-8a,
=2a(a2-4),
=2a(a+2)(a-2);
(2)4a(x-y)-2b(y-x),
=4a(x-y)+2b(x-y),
=2(x-y)(2a+b);
(3)(x2+4)2-16x2,
=(x2+4x+4)(x2-4x+4),
=(x+2)2(x-2)2;
(4)(x-y)2+4xy,
=x2-2xy+y2+4xy,
=x2+2xy+y2,
=(x+y)2.
点评 本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
相关题目
18. 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )| A. | a=2b | B. | a=3b | C. | a=3.5b | D. | a=4b |
8.如果把$\frac{5x}{x+y}$中的x与y都扩大为原来的5倍,那么这个代数式的值( )
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 缩小为原来的$\frac{1}{5}$ | D. | 扩大为原来的10倍 |
12.下列调查适合作普查的是( )
| A. | 了解在校大学生的主要娱乐方式 | |
| B. | 了解“嫦娥三号”卫星零部件的状况 | |
| C. | 日光灯管厂要检测一批灯管的使用寿命 | |
| D. | 了解某市居民对废电池的处理情况 |
13.下列各式中,不能用平方差公式计算的是( )
| A. | (-x-y)(x-y) | B. | (-x+y)(-x-y) | C. | (x+y)(-x+y) | D. | (x-y)(-x+y) |
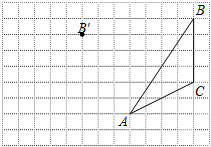 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算: 实数a在数轴上的位置如图所示,化简$\sqrt{{a^2}-2a+1}$+|2a-4|=3-a.
实数a在数轴上的位置如图所示,化简$\sqrt{{a^2}-2a+1}$+|2a-4|=3-a.